
 已知,某一次函數與反比例函數相交于A(1,3),B(m,1),求:
已知,某一次函數與反比例函數相交于A(1,3),B(m,1),求:分析 (1)設一次函數與反比例函數的解析式分別為y=ax+b(k≠0),y=$\frac{k}{m}$(k≠0),將A坐標代入反比例解析式中求出k的值,確定出反比例解析式,再將B坐標代入反比例解析式中求出m的值,確定出B坐標,將A與B坐標代入一次函數解析式中求出a與b的值,即可確定出一次函數解析式;
(2)設一次函數與x軸交于C點,求出C坐標,三角形AOB的面積=三角形AOC-三角形BOC的面積,求出即可.
解答 解:(1)設一次函數與反比例函數的解析式分別為y=ax+b(k≠0),y=$\frac{k}{m}$(k≠0),
∵反比例函數y=$\frac{k}{m}$(k≠0)的圖象經過點A(1,3),
∴k=1×3=3,
∴反比例函數的解析式為y=$\frac{3}{x}$,
∵點B(m,1)在反比例函數的圖象上,
∴1=$\frac{3}{m}$
∴m=3,
∴點B的坐標為(3,1),
∵一次函數的圖象經過點A,B,
將這兩個點的坐標代入y=kx+b,得$\left\{\begin{array}{l}{3=a+b}\\{1=3a+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
則所求一次函數的解析式為y=-x+4;
(2)設一次函數y=-x+4的圖象交x軸于點C,
∴C點坐標為(4,0),即OC=4,
∵A點的縱坐標為3,B點的縱坐標為1,
∴S△AOB=S△AOC-S△BOC=$\frac{1}{2}$OC•3-$\frac{1}{2}$OC•1=$\frac{1}{2}$×4×2=4.
點評 此題考查了一次函數與反比例函數的交點問題,涉及的知識有:待定系數法確定函數解析式,一次函數與x軸的交點,坐標與圖形性質,以及三角形的面積求法,熟練掌握待定系數法是解本題的關鍵.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
 如圖,在這個漂亮的螺旋圖中,所有的三角形都是直角三角形,按此方式繼續畫下去:根據圖中所標數據.
如圖,在這個漂亮的螺旋圖中,所有的三角形都是直角三角形,按此方式繼續畫下去:根據圖中所標數據.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3.94×103 | B. | 3.94×104 | C. | 39.4×103 | D. | 0.394×105 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{9}{10}$a元 | B. | $\frac{10}{9}$a元 | C. | $\frac{1}{10}$a元 | D. | 10a元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某校八年級以“我最喜愛的體育運動”為主題對該校八年級每位學生進行了調查,調查的運動項目有:籃球、羽毛球、乒乓球、跳繩及其它項目(每位同學僅選一項),經調查每位同學都做了選擇,根據調查結果繪制如下統計圖表:
某校八年級以“我最喜愛的體育運動”為主題對該校八年級每位學生進行了調查,調查的運動項目有:籃球、羽毛球、乒乓球、跳繩及其它項目(每位同學僅選一項),經調查每位同學都做了選擇,根據調查結果繪制如下統計圖表:| 運動項目 | 頻數 |
| 籃球 | 90 |
| 羽毛球 | m |
| 乒乓球 | 108 |
| 跳繩 | 54 |
| 其它 | n |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
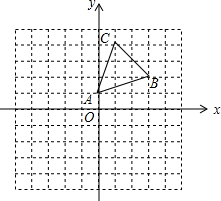 如圖,△ABC的頂點均在正方形網格的格點上,在已知的直角坐標系中,A(0,1),B(3,2).
如圖,△ABC的頂點均在正方形網格的格點上,在已知的直角坐標系中,A(0,1),B(3,2).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 由一些大小相同的小正方形組成的幾何體俯視圖和左視圖如圖所示,那么,組成這個幾何體的小正方體個數可能有( )
由一些大小相同的小正方形組成的幾何體俯視圖和左視圖如圖所示,那么,組成這個幾何體的小正方體個數可能有( )| A. | 8塊 | B. | 6塊 | C. | 4塊 | D. | 12塊 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com