日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情
如圖，利用四邊形的不穩定性改變矩形ABCD的形狀，得到?A1BCD1，若?A1BCD1的面積是矩形ABCD面積的一半，則∠ABA1的度數是（ ）

A．15°
B．30°
C．45°
D．60°
【答案】分析：過A1作A1H⊥BC于H，根據?A1BCD1的面積是矩形ABCD面積的一半，求出A1H=A1B，根據含30度角的直角三角形性質求出∠A1BH=30°即可．
解答：
解：過A1作A1H⊥BC于H，
∵?A1BCD1的面積是矩形ABCD面積的一半，
∴AB×BC=2BC×A1H，
∴A1H=A1B，
∴∠A1BH=30°，
∴∠ABA1=90°-30°=60°，
故選D．
點評：本題考查了含30度角的直角三角形性質，矩形的性質和平行四邊形的性質等知識點的應用，關鍵是求出A1H=A1B，用的數學數學是轉化思想，即把實際問題轉化成數學問題．
練習冊系列答案
相關習題

科目：初中數學 來源： 題型：閱讀理解

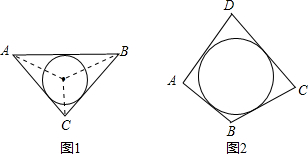精英家教網閱讀材料：如圖1，△ABC的周長為l，面積為S，內切圓O的半徑為r，探究r與S、l之間的關系．連接OA，OB，OC∵S=S△OAB+S△OBC+S△OCA
又∵S△OAB=
1
2
AB•r，S△OBC=
1
2
BC•r，S△OCA=
1
2
CA•r
∴S=
1
2
AB•r+
1
2
BC•r+
1
2
CA•r=
1
2
l•r
∴r=
2S
l

解決問題：
（1）利用探究的結論，計算邊長分別為5，12，13的三角形內切圓半徑；
（2）若四邊形ABCD存在內切圓（與各邊都相切的圓），如圖2且面積為S，各邊長分別為a，b，c，d，試推導四邊形的內切圓半徑公式；
（3）若一個n邊形（n為不小于3的整數）存在內切圓，且面積為S，各邊長分別為a1，a2，a3，…，an，合理猜想其內切圓半徑公式（不需說明理由）．

查看答案和解析>>

科目：初中數學 來源： 題型：

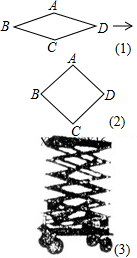（2011•朝陽）如圖（3）是利用四邊形的不穩定性制造的一個移動升降裝修平臺，其基本圖形是菱形，主體部分相當于由6個菱形相互連接而成，通過改變菱形的角度，從而可改變裝修平臺高度．
（1）如圖（1）是一個基本圖形，已知AB=1米，當∠ABC為30°時，求AC的長及此時整個裝修平臺的高度（裝修平臺的基腳高度忽略不計）；
（2）當∠ABC從30°變為90°（如圖（2）是一個基本圖形變化后的圖形）時，求整個裝修平臺升高了多少米．
[結果精確到0.1米，參考數據：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，
2
≈1.41]．

查看答案和解析>>

科目：初中數學 來源：遼寧省朝陽市2011年初中畢業升學考試數學試卷 題型：044

如圖是利用四邊形的不穩定性制造的一個移動升降裝修平臺，其基本圖形是菱形，主體部分相當于由6個菱形相互連接而成，通過改變菱形的角度，從而可改變裝修平臺高度．

(1)如圖是一個基本圖形，已知AB＝1米，當∠ABC為30°時，求AC的長及此時整個裝修平臺的高度(裝修平臺的基腳高度忽略不計)；

(2)當∠ABC從30°變為90°(如圖是一個基本圖形變化后的圖形)時，求整個裝修平臺升高了多少米．

[結果精確到0.1米，參考數據：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，≈1.41]

查看答案和解析>>

科目：初中數學 來源：2011-2012學年江蘇省太倉市七年級期中考試數學卷（帶解析） 題型：解答題

探究與發現：
探究一：我們知道，三角形的一個外角等于與它不相鄰的兩個內角的和．那么，三角形的一個內角與它不相鄰的兩個外角的和之間存在何種數量關系呢？已知：如圖，∠FDC與∠ECD分別為△ADC的兩個外角，試探究∠A與∠FDC+∠ECD的數量關系．

探究二：三角形的一個內角與另兩個內角的平分線所夾的鈍角之間有何種關系？
已知：如圖，在△ADC中，DP、CP分別平分∠ADC和∠ACD，試探究∠P與∠A的數量關系．

探究三：若將△ADC改為任意四邊形ABCD呢？
已知：如圖，在四邊形ABCD中，DP、CP分別平分∠ADC和∠BCD，試利用上述結論探究∠P與∠A+∠B的數量關系．

探究四：若將上題中的四邊形ABCD改為六邊形ABCDEF呢？
請直接寫出∠P與∠A+∠B+∠E+∠F的數量關系：_______________________________．

查看答案和解析>>

科目：初中數學 來源：2011-2012學年江蘇省太倉市七年級下學期期中考試數學試卷（帶解析） 題型：解答題

探究與發現：
探究一：我們知道，三角形的一個外角等于與它不相鄰的兩個內角的和．那么，三角形的一個內角與它不相鄰的兩個外角的和之間存在何種數量關系呢？
已知：如圖，∠FDC與∠ECD分別為△ADC的兩個外角，
試探究∠A與∠FDC+∠ECD的數量關系．

探究二：三角形的一個內角與另兩個內角的平分線所夾的鈍角之間有何種關系？
已知：如圖，在△ADC中，DP、CP分別平分∠ADC和∠ACD，試探究∠P與∠A的數量關系．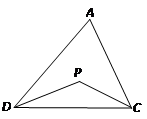

探究三：若將△ADC改為任意四邊形ABCD呢？
已知：如圖，在四邊形ABCD中，DP、CP分別平分∠ADC和∠BCD，試利用上述結論探究∠P與∠A+∠B的數量關系．

探究四：若將上題中的四邊形ABCD改為六邊形ABCDEF呢？
請直接寫出∠P與∠A+∠B+∠E+∠F的數量關系： _______________________________．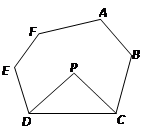

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 欧美日韩激情在线一区二区三区 | 91久久精品一区二区二区 | 中文字幕一区日韩精品欧美 | 91精品久久久久久久久久 | 五月天最新网址 | 国产高清精品一区二区三区 | 国产精品视频一区二区三区不卡 | 国产a久久精品一区二区三区 | 在线va | 亚洲综合激情网 | 精品中文字幕一区二区三区 | 亚洲免费观看视频 | 久久久久久成人精品 | 国产在线国偷精品产拍免费yy | 最新日韩视频 | 亚洲免费在线观看视频 | 亚洲精品一区二区三区麻豆 | 亚洲 欧美 在线 一区 | 国产成人一区二区三区 | 日韩中文字幕一区 | 欧美在线综合 | 国产精品久久久久久久娇妻 | 爱啪视频 | 日本久久二区 | 午夜大片网 | 精品久久影院 | 久久精品国产一区二区电影 | 日韩国产在线观看 | 农村少妇一级片 | 日韩视频免费在线观看 | 91免费版在线观看 | 国产精品久久久久久久久久久久午夜片 | 九九热精品视频在线 | 国产精品欧美三级在线观看 | 国产精品久久久久久一区二区三区 | 欧美日韩黄色一区二区 | 精品欧美一区二区在线观看 | 国产成人精品一区二 | www.久久 | 日本在线不卡视频 | 亚洲黄色毛片 |