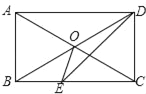
【題目】如圖，在四邊形ABCD中，AD∥BC，∠ABC=∠ADC=90°，對角線AC，BD交于點O，DE平分∠ADC交BC于點E，連接OE．
（1）求證：四邊形ABCD是矩形；
（2）若AB=2，求△OEC的面積．
【答案】（1）證明見解析；（2）1.
【解析】分析：（1）只要證明三個角是直角即可解決問題；
（2）作OF⊥BC于F．求出EC、OF的長即可；
詳解：（1）證明：∵AD∥BC，
∴∠ABC+∠BAD=180°，
∵∠ABC=90°，
∴∠BAD=90°，
∴∠BAD=∠ABC=∠ADC=90°，
∴四邊形ABCD是矩形．
（2）作OF⊥BC于F．
∵四邊形ABCD是矩形，
∴CD=AB=2，∠BCD=90°，AO=CO，BO=DO，AC=BD，
∴AO=BO=CO=DO，
∴BF=FC，
∴OF=
CD=1，
∵DE平分∠ADC，∠ADC=90°，
∴∠EDC=45°，
在Rt△EDC中，EC=CD=2，
∴△OEC的面積=ECOF=1．
課課練江蘇系列答案
名牌中學課時作業系列答案科目：初中數學 來源： 題型：
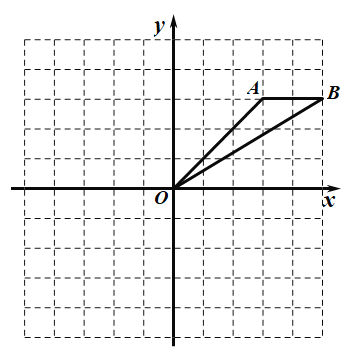
【題目】如圖，在平面直角坐標系中，已知點A（3，3），B（5，3）．
（1）已知點C（2，－4），求四邊形AOCB的面積；
（2）將線段OB先向上平移2個單位長度，再向左平移4個單位長度，得到線段O2B2，畫出兩次平移后的圖形，并求線段OB在兩次平移過程中掃過的總面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點
是數軸上的兩點，
為原點，點
表示的數是1，點
在點的左側，
．
（1）求點表示的數；
（2）數軸上的一點
在點的右側，設點表示的數是
，若點到，兩點的距離的和是15，求的值；
（3）動點
從點出發，以每秒2個單位的速度向右運動，同時動點
從點出發，以每秒1個單位的速度向右運動，設運動時間為
秒，是否存在這樣的值，使
，若存在，請求出的值，若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
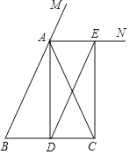
【題目】已知：如圖，在△ABC中，AB＝AC，AD是△ABC的中線，AN為△ABC的外角∠CAM的平分線，CE∥AD，交AN于點E．求證：四邊形ADCE是矩形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分線BE交AC的延長線于點E．
（1）求∠CBE的度數；
（2）過點D作DF∥BE，交AC的延長線于點F，求∠F的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
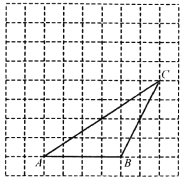
【題目】如圖，在每個小正方形邊長為1的方格紙中，△
的頂點都在方格紙格點上.將△向左平移2格，再向上平移4格．
（1）請在圖中畫出平移后的△
;
（2）圖中AC和
的關系 ；
（3）再在圖中畫出△的高
;
（4）
= ；
（5）在圖中能使
的格點
的個數有 個(點異于C)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，過半徑為6的圓O上一點A作圓O的切線l，P為圓O的一個動點，作PH⊥l于點H，連接PA．如果PA=x，AH=y，那么下列圖象中，能大致表示y與x的函數關系的是（ ）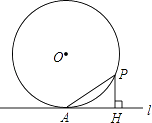
A.
B.
C.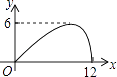
D.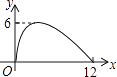
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
