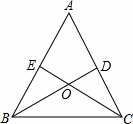
日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情

如圖，在△ABC中，點D，E分別在邊AC，AB上，BD與CE交于點O，給出下列三個條件：①∠EBO=∠DCO；②BE=CD；③OB=OC．

（1）上述三個條件中，由哪兩個條件可以判定△ABC是等腰三角形？（用序號寫出所有成立的情形）

（2）請選擇（1）中的一種情形，寫出證明過程．

　


解：（1）①②；①③．

（2）選①③證明如下，

∵OB=OC，

∴∠OBC=∠OCB，

∵∠EBO=∠DCO，

又∵∠ABC=∠EBO+∠OBC，∠ACB=∠DCO+∠OCB，

∴∠ABC=∠ACB，

∴△ABC是等腰三角形．

　

練習冊系列答案
相關習題

科目：初中數學 來源： 題型：


如圖，直線AB的解析式為y=2x+4，交x軸于點A，交y軸于點B，以A為頂點的拋物線交直線AB于點D，交y軸負半軸于點C（0，-4），

（1）求拋物線解析式；

（2）將拋物線頂點沿著直線AB平移，此時頂點記為E，與y軸的交點記為F，求當△BEF與△BAO相似時，E點坐標；

（3）記平移后拋物線與AB另一個交點為G，則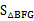與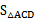是否存在8倍的關系，若有，寫出F點坐標。

　

查看答案和解析>>

科目：初中數學 來源： 題型：


如圖，正方形ABCD邊長為1，當M、N分別在BC，CD上，使得△CMN的周長為2，則△AMN的面積的最小值為           .

　

查看答案和解析>>

科目：初中數學 來源： 題型：


用一條長40cm的繩子圍成一個面積為64cm2的長方形．設長方形的長為xcm，則可列方程為（　　）

　

A．

x（20+x）=64

B．

x（20﹣x）=64

C．

x（40+x）=64

D．

x（40﹣x）=64

　

查看答案和解析>>

科目：初中數學 來源： 題型：


若正數a是一元二次方程x2﹣5x+m=0的一個根，﹣a是一元二次方程x2+5x﹣m=0的一個根，則a的值是　　

查看答案和解析>>

科目：初中數學 來源： 題型：


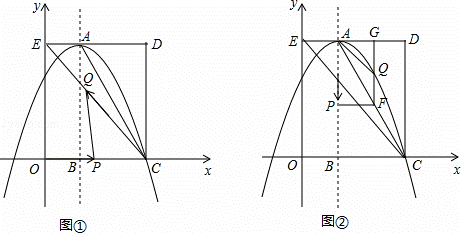
如圖，在平面直角坐標系中，矩形OCDE的三個頂點分別是C（3，0），D（3，4），E（0，4）．點A在DE上，以A為頂點的拋物線過點C，且對稱軸x=1交x軸于點B．連接EC，AC．點P，Q為動點，設運動時間為t秒．

（1）填空：點A坐標為　 　；拋物線的解析式為　 　．

（2）在圖1中，若點P在線段OC上從點O向點C以1個單位/秒的速度運動，同時，點Q在線段CE上從點C向點E以2個單位/秒的速度運動，當一個點到達終點時，另一個點隨之停止運動．當t為何值時，△PCQ為直角三角形？

（3）在圖2中，若點P在對稱軸上從點A開始向點B以1個單位/秒的速度運動，過點P做PF⊥AB，交AC于點F，過點F作FG⊥AD于點G，交拋物線于點Q，連接AQ，CQ．當t為何值時，△ACQ的面積最大？最大值是多少？

　

查看答案和解析>>

科目：初中數學 來源： 題型：


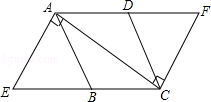
如圖，菱形ABCD的邊長為4，過點A、C作對角線AC的垂線，分別交CB和AD的延長線于點E、F，AE=3，則四邊形AECF的周長為（  ）

 

　

A．

22

B．

18

C．

14

D．

11

  

查看答案和解析>>

科目：初中數學 來源： 題型：


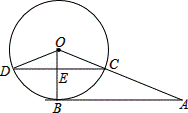
如圖，A為⊙O外一點，AB切⊙O于點B，AO交⊙O于C，CD⊥OB于E，交⊙O于點D，連接OD．若AB=12，AC=8．

（1）求OD的長；

（2）求CD的長．

 

  

查看答案和解析>>

科目：初中數學 來源： 題型：


如圖，在▱ABCD中，F是BC上的一點，直線DF與AB的延長線相交于點E，BP∥DF，且與AD相交于點P，請從圖中找出一組相似的三角形：            

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 女人夜夜春高潮爽a∨片传媒 | 日韩一区二区不卡 | 偷拍自拍亚洲 | www成人精品 | 久久av一区二区三区 | av在线播放网站 | 色婷婷综合久久久久中文 | 欧美日韩高清丝袜 | 最新日韩在线观看视频 | 中文字幕久久精品 | 国产精品久久久久久久久久久久冷 | 国产成人精品免费 | 久久久久国产精品午夜一区 | 亚洲九九 | 国产精品久久久久久久久久久久冷 | 色爽女人免费 | 久久久久久久一区 | 欧美日韩国产精品 | 久久久久女人精品毛片九一韩国 | 一级毛片aaaaaa免费看 | 欧美激情综合色综合啪啪五月 | 米奇狠狠狠狠8877 | 国产精品久久久久久久久免费高清 | 99热精品在线| 欧美一级在线 | 国产精品一区二区欧美 | 日韩色| 久久理论片 | 激情欧美一区二区 | 天堂一区二区三区四区 | 国产精品久久久久毛片软件 | 在线不卡日本 | 午夜理伦三级 | 国产传媒在线观看 | 婷婷综合网 | 国产91在线观看 | 成人在线h | av2014天堂网| 国产精品国色综合久久 | 婷婷久久综合 | 精品国产乱码一区二区三 |