
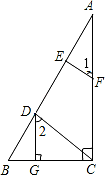
已知:如下圖,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求證:CD⊥AB。
證明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定義)
∴DG∥AC( )
∴∠2=( )( )
∵∠1=∠2(已知)
∴∠1=∠( )(等量代換)
∴EF∥CD( )
∴∠AEF=∠( )( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
科目:初中數學 來源:江蘇省姜堰市2012屆九年級上學期期中考試數學試題 題型:044
如圖,已知正方形ABCD,將一個45度角∝的頂點放在D點并繞D點旋轉,角的兩邊分別交AB邊和BC邊于點E和F,連接EF.求證:EF=AE+CF
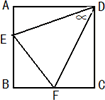
(1)小明是這樣思考的:延長BC到G,使得CG=AE,連接DG,先證△DAE≌△DCG,再證△DEF≌△DGF,請你借助下圖,按照小明的思路,寫出完整的證明思路.

(2)劉老師看到這條題目后,問了小明兩個小問題:①如果正方形的邊長和△BEF的面積都等于6,求EF的長②將角∝繞D點繼續旋轉,使得角∝的兩邊分別和AB邊延長線、BC邊的延長線交于E和F,如圖所示,猜想EF、AE、CF三線段之間的數量關系并給予證明.請你幫忙解決.

查看答案和解析>>
科目:初中數學 來源:非常講解·教材全解全析 數學 九年級下 (配北師大課標) 配北師大課標 題型:044
已知二次函數y=mx2+3(m-![]() )x+4(m<0),與x軸交于A,B兩點(A在B的左邊),與y軸交于點C,并且∠ACB=90°,如下圖所示,
)x+4(m<0),與x軸交于A,B兩點(A在B的左邊),與y軸交于點C,并且∠ACB=90°,如下圖所示,
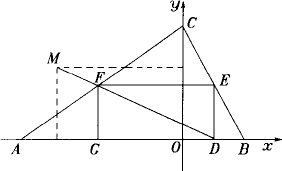
(1)求這個二次函數的解析式;
(2)矩形DEFG的一條邊DG在AB上,E,F分別在BC,AC上,設OD=x(x>0),矩形DEFG的面積為S,求S與x的函數關系式;
(3)當矩形DEFG的面積S最大時,連結對角線DF并延長到M,使FM=![]() DF,試判斷此時點M是否在二次函數y=mx2+3(m-
DF,試判斷此時點M是否在二次函數y=mx2+3(m-![]() )x+4的圖象上?請說明理由.
)x+4的圖象上?請說明理由.
查看答案和解析>>
科目:初中數學 來源:學習周報 數學 滬科九年級版 2009-2010學年 第14期 總第170期 滬科版 題型:044
已知正方形
ABCD和正方形AEFG有一個公共點A,點G、E分別在線段AD、AB上.(1)如下圖,連接DF、BF.若將正方形AEFG繞點A按順時針方向旋轉,請你判斷命題“在旋轉的過程中線段DF與BF的長度始終相等”是否正確,若正確,請說明理由;若不正確,請舉反例說明;

(2)若將正方形AEFG繞點A按順時針方向旋轉,連接DG,如下圖.在旋轉的過程中,你能否找到一條線段與線段DG的長度始終相等?并說明理由

查看答案和解析>>
科目:初中數學 來源:同步題 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com