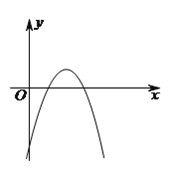
【題目】（
分）如圖，拋物線
的頂點為
．
（
）求拋物線
的函數表達式．
（
）若拋物線形
與
關于
軸對稱，求拋物線
的函數表達式．
（
）在（
）的基礎上，設
上的點
、
始終與
上的點
、
分別關于
軸對稱，是否存在點
、
（
、
分別位于拋物線對稱軸兩側，且
在
的左側），使四邊形
為正方形？
若存在，求出點
的坐標；若不存在，說明理由．
【答案】（1）y=-x2+6x-7;(2)y=x2-6x+7;(3)存在，（2,1）或（1，-2）
【解析】試題分析： 
根據頂點坐標，求出
的值，求拋物線
的函數表達式．
拋物線
與
關于
軸對稱，求出拋物線
的頂點坐標和二次項系數，即可求得函數表達式.
根據正方形的邊長相等, 
．列出方程，求解即可.
試題解析：
（
）拋物線
的頂點為
．
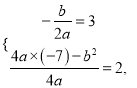
解得： 
．
（
）若拋物線
的頂點坐標為
． 
若拋物線
與
關于
軸對稱，
拋物線
的頂點坐標為： 
拋物線
的函數表達式為：
．
（
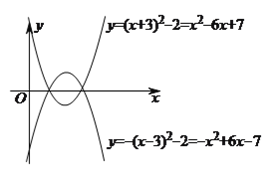
）存在．
如圖，要使四邊形
是正方形，
∵
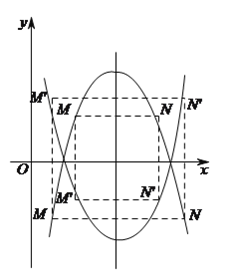
軸，則要
軸，
且
．
設
， 
，
∵拋物線的對稱軸為：直線
，
∴由拋物線的對稱性可知
，
∴
．
當
，
解得： 
，（ 
舍去），此時
，
當
時， 
，
解得： 
，（ 
舍去），此時
，
綜上，存在這樣的點
或
．
科目：初中數學 來源： 題型：
【題目】某餐廳中，一張桌子可坐6人，有如圖所示的兩種擺放方式：
（1）當有n張桌子時，兩種擺放方式各能坐多少人？
（2）一天中午餐廳要接待98位顧客共同就餐，但餐廳只有25張這樣的餐桌.若你是這個餐廳的經理，你打算選擇哪種方式來擺放餐桌？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，EF//AB，GH//BC，EF、GH的交點P在BD上，圖中面積相等的矩形有( )
A.1對B.2對C.3對D.4對
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】體育課上，小明、小強、小華三人在學習訓練踢足球，足球從一人傳到另一人就記為踢一次．
(1)如果從小強開始踢，經過兩次踢球后，足球踢到了小華處的概率是多少(用樹狀圖或列表的方法加以說明)?
(2)如果踢三次后，球踢到了小明處的可能性最小，應從誰開始踢？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題滿分
分）小明、小華在一棟高樓前感慨樓房真高．小明說：“這樓起碼
層！”小華卻不以為然：“
層？我看沒有！”小明說：“有本事，就讓我們一起來測量吧！”
如圖，矩形
表示樓體，小明、小華在樓體兩側各選
、
兩點，使得
、
、
、
四點在同一直線上，利用皮尺和側傾器測得如下數據， 
米， 
米， 
， 
．
（
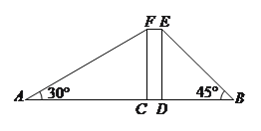
）請你幫助他們算一算樓高．（結果保留根號）
（
）若每層樓按
米計算，你支持小明還是小華的觀點呢？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（
分）在菱形
中， 
， 
，點
是線段
上的一個動點．
（
）如圖①，求
的最小值．
（
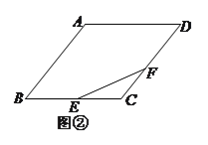
）如圖②，若
也是
邊上的一個動點，且
，求
的最小值．
（
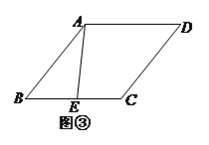
）如圖③，若
，則在菱形內部存在一點
，使得點
分別到點
、點
、邊
的距離之和最小．請你畫出這樣的點
，并求出這個最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】四邊形ABCD中，對角線AC、BD相交于點O，下列條件不能判定這個四邊形是平行四邊形的是
A．AB∥DC，AD∥BC B．AB=DC，AD=BC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，Rt△ABC中，AB=AC=8，BO=
AB，點M為BC邊上一動點，將線段OM繞點O按逆時針方向旋轉90°至ON，連接AN、CN，則△CAN周長的最小值為________.
查看答案和解析>>
科目：初中數學 來源： 題型：
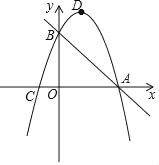
【題目】已知，如圖，拋物線y=﹣x2+bx+c經過直線y=﹣x+3與坐標軸的兩個交點A，B，此拋物線與x軸的另一個交點為C，拋物線的頂點為D．
（1）求此拋物線的解析式；
（2）若點M為拋物線上一動點，是否存在點M，使△ACM與△ABC的面積相等？若存在，求點M的坐標；若不存在，請說明理由．
（3）在x軸上是否存在點N使△ADN為直角三角形？若存在，確定點N的坐標；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com