
【題目】已知![]() ,
,![]() .
.
(1)若![]() ,作
,作![]() ,點
,點![]() 在
在![]() 內.
內.
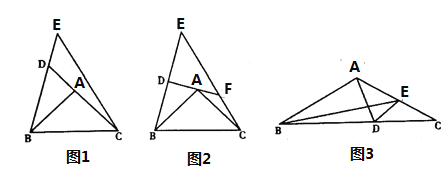
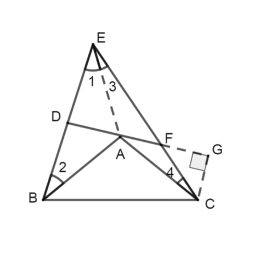
①如圖1,延長![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的度數為 ;
的度數為 ;
②如圖2,![]() 垂直平分
垂直平分![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,求
,求![]() 的值;
的值;
(2)如圖3,若![]() ,點
,點![]() 在
在![]() 邊上,
邊上,![]() ,點
,點![]() 在
在![]() 邊上,連接
邊上,連接![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
【答案】(1)①15°;②![]() ;(2)
;(2)![]()
【解析】
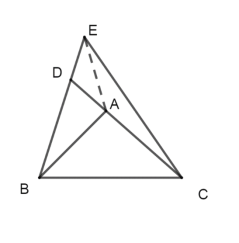
(1)①根據等腰直角三角形的性質,連接![]() ,得
,得![]() ,
,![]() ,
,![]() 所對的直角邊是斜邊的一半,可得
所對的直角邊是斜邊的一半,可得![]() ,所以可得,
,所以可得,![]() ,
,![]() ,
,![]() 和
和![]() 是等腰三角形,由外角性質計算可得;
是等腰三角形,由外角性質計算可得;
②構造“一線三垂直”模型,證明三角形![]() ,利用面積比等于等高的三角形的底邊的比,結合已知條件即可解得.
,利用面積比等于等高的三角形的底邊的比,結合已知條件即可解得.
(2)構造等邊![]() ,通過證明
,通過證明![]() ,等邊代換,得出等腰三角形
,等邊代換,得出等腰三角形![]() ,代入角度計算即得.
,代入角度計算即得.
(1)①連接AE,在![]() ,因為
,因為![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案為:![]() .
.
②過C作![]() 交DF延長線于G,連接AE
交DF延長線于G,連接AE
![]() AD垂直平分BE,
AD垂直平分BE,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
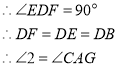
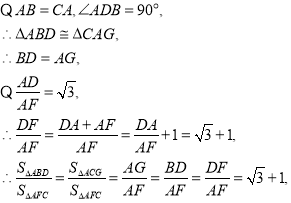
故答案為:![]() ;
;
(2)以AB向下構造等邊![]() ,連接DK,
,連接DK,
延長AD,BK交于點T,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
等邊![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
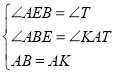
![]() ,
,
![]()
等邊三角形三線合一可知,BD是邊AK的垂直平分線,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案為:![]() .
.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:初中數學 來源: 題型:
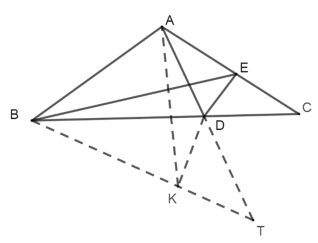
【題目】如圖,在△ABC中,∠B、∠C的平分線BE,CD相交于點F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度數;
(2)直接寫出∠A與∠BFD的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
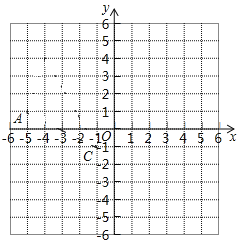
【題目】如圖,在平面直角坐標系xOy中,△ABC三個頂點都在格點上,且坐標分別為A(-2,4),B(-2,1),C(-5,2).
(1)在坐標系中,標出三個頂點坐標,并畫出△ABC;
(2)作出△ABC關于x軸對稱的△A1B1C1;
(3)將![]() 的三個頂點的橫坐標和縱坐標同時乘以
的三個頂點的橫坐標和縱坐標同時乘以![]() ,得到對應的點
,得到對應的點![]() 、
、![]() 、
、![]() ,畫出
,畫出![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是二次函數y=ax2+bx+c的部分x,y的對應值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函數圖象的頂點坐標是 ;
(2)當拋物線y=ax2+bx+c的頂點在直線y=x+n的下方時,n的取值范圍是 。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】金瑞公司決定從廠家購進甲、乙兩種不同型號的顯示器共50臺,購進顯示器的總金額不超過77000元,已知甲、乙型號的顯示器價格分別為1000元/臺、2000元/臺.
(1)求金瑞公司至少購進甲型顯示器多少臺?
(2)若甲型顯示器的臺數不超過乙型顯示器的臺數,則有哪些購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
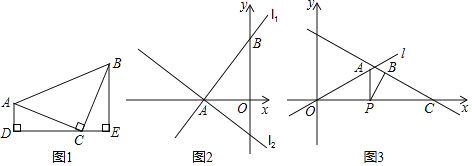
【題目】(模型建立)
(1)如圖1,等腰直角三角形ABC中,∠ACB=90°,CA=CB,直線ED經過點C,過A作AD⊥ED于點D,過B作BE⊥ED于點E.
求證:△CDA≌△BEC.
(模型運用)
(2)如圖2,直線l1:y=![]() x+4與坐標軸交于點A、B,將直線l1繞點A逆時針旋轉90°至直線l2,求直線l2的函數表達式.
x+4與坐標軸交于點A、B,將直線l1繞點A逆時針旋轉90°至直線l2,求直線l2的函數表達式.
(模型遷移)
如圖3,直線l經過坐標原點O,且與x軸正半軸的夾角為30°,點A在直線l上,點P為x軸上一動點,連接AP,將線段AP繞點P順時針旋轉30°得到BP,過點B的直線BC交x軸于點C,∠OCB=30°,點B到x軸的距離為2,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB = 6cm,∠CAB = 25°,P是線段AB上一動點,過點P作PM⊥AB交射線AC于點M,連接MB,過點P作PN⊥MB于點N.設A,P兩點間的距離為xcm,P,N兩點間的距離為ycm.(當點P與點A或點B重合時,y的值均為0)小海根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.

下面是小海的探究過程,請補充完整:
(1)通過取點、畫圖、測量,得到了x與y的幾組值,如下表:
x/cm | 0.00 | 0.60 | 1.00 | 1.51 | 2.00 | 2.75 | 3.00 | 3.50 | 4.00 | 4.29 | 4.90 | 5.50 | 6.00 |
y/cm | 0.00 | 0.29 | 0.47 | 0.70 | 1.20 | 1.27 | 1.37 | 1.36 | 1.30 | 1.00 | 0.49 | 0.00 |
(說明:補全表格時相關數值保留兩位小數)
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:當y=0.5時,與之對應的![]() 值的個數是 .
值的個數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一個根,求m的值及另一個根;
(2)當m為何值時方程有兩個不同的實數根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com