
分析 (1)原式括號中兩項通分并利用同分母分式的減法法則計算,同時利用除法法則變形,約分即可得到結果;
(2)原式括號中兩項通分并利用同分母分式的加法法則計算,同時利用除法法則變形,約分即可得到結果.
解答 解:(1)原式=$\frac{{a}^{2}+4a+4-{a}^{2}-8}{{a}^{2}+4a+4}$•$\frac{a(a+2)}{4(a-1)}$=$\frac{4(a-1)}{(a+2)^{2}}$•$\frac{a(a+2)}{4(a-1)}$=$\frac{a}{a+2}$;
(2)原式=$\frac{m+1}{m}$•$\frac{(m-1)^{2}}{(m+1)(m-1)}$=$\frac{m-1}{m}$.
點評 此題考查了分式的混合運算,熟練掌握運算法則是解本題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2016-2017學年河南省七年級下學期第一次月考(3月)數學試卷(解析版) 題型:填空題
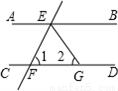
如圖,AB∥CD,直線EF分別交AB、CD于E、F,EG平分∠BEF,若∠1=72°,則∠2= ______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com