
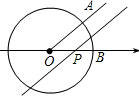
 如圖,已知⊙O是以數軸的原點O為圓心,半徑為1的圓,∠AOB=45°,點P在數軸上運動,若過點P且與OA平行的直線與⊙O有公共點,設OP=x,則x的取值范圍是0<x≤$\sqrt{2}$.
如圖,已知⊙O是以數軸的原點O為圓心,半徑為1的圓,∠AOB=45°,點P在數軸上運動,若過點P且與OA平行的直線與⊙O有公共點,設OP=x,則x的取值范圍是0<x≤$\sqrt{2}$. 分析 根據題意,知直線和圓有公共點,則相切或相交.相切時,設切點為C,連接OC.根據等腰直角三角形的直角邊是圓的半徑1,求得斜邊是$\sqrt{2}$,所以x的取值范圍是0≤x≤$\sqrt{2}$.
解答 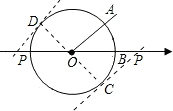 解:設切點為C,連接OC,則圓的半徑OC=1,OC⊥PC,
解:設切點為C,連接OC,則圓的半徑OC=1,OC⊥PC,
∵∠AOB=45°,OA∥PC,
∴∠OPC=45°,
∴PC=OC=1,
∴OP=$\sqrt{2}$,
同理,原點左側的距離也是$\sqrt{2}$,且線段是正數,
∴x的取值范圍是0<x≤$\sqrt{2}$.
故答案為:0<x≤$\sqrt{2}$.
點評 此題主要考查了直線與圓的位置關系,分別得出兩圓與圓相切時求出OP的長是解決問題的關鍵,難度一般,注意兩個極值點的尋找.


科目:初中數學 來源: 題型:選擇題
| A. | 任何兩個互為相反數的數的商為-1 | |
| B. | 任何一個不是1的正數都大于它的倒數 | |
| C. | 若a>b>0,則$\frac{1}{a}>\frac{1}{b}$ | |
| D. | 若$\frac{1}{a}<-1$,則-1<a<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com