
【題目】如圖,某中學準備在校園里利用院墻的一段再圍三面籬笆,形成一個矩形花園![]() (院墻
(院墻![]() 長
長![]() 米),現有
米),現有![]() 米長的籬笆.
米長的籬笆.

(1)請你設計一種圍法(籬笆必須用完),使矩形花園的面積為![]() 米.
米.
(2)如何設計可以使得圍成的矩形面積最大?最大面積是多少?
【答案】見詳解.
【解析】
(1)設AB為xm,則BC為(40-2x)m,根據題意可得等量關系:矩形的面積=長×寬=150,根據等量關系列出方程,再解即可;
(2)根據題意和圖形可以得到S與x之間的函數關系,將函數關系式化為頂點式,即可解答本題.
解:(1)設AB為xm,則BC為(40-2x)m,根據題意可得:
X(40-2x)=150
解得:x1=![]() ,x2=15.
,x2=15.
:當x=![]() 時,40-2x=30>25.故不滿足題意,應舍去.
時,40-2x=30>25.故不滿足題意,應舍去.
②當x=15時,40-2x=10<25,故當x=15時,滿足實際要求.
∴當x=15 時,使矩形花園的面積為![]() 米.
米.
(2)設矩形的面積為S,則依意得:
S= X(40-2x)=-2x2+40x=-2(x-5)2+50
∴當x=5,時S有最大值.最大值為50.


科目:初中數學 來源: 題型:
【題目】為鼓勵居民節約用電,某市采用價格調控手段達到省電目的,該市電費收費標準如下表(按月結算):
每月用電量度 | 電價/(元/度) |
不超過150度的部分 | 0.50元/度 |
超過150度且不超過250度的部分 | 0.65元/度 |
超過250度的部分 | 0.80元/度 |
問:(1)某居民12月份用電量為180度,請問該居民12月應繳交電費多少元?
(2)設某月的用電量為![]() 度(
度(![]() ),試寫出不同電量區間應繳交的電費.
),試寫出不同電量區間應繳交的電費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強公民的節水意識,合理利用水資源,某區采用價格調控手段達到節水的目的,如表是調控后的價目表.
價目表
每月用水量 | 單價 |
不超過6噸的部分 | 2元/噸 |
超出6噸不超出10噸的部分 | 4元/噸 |
超出10噸的部分 | 8元/噸 |
注:水費按月結算.
(1)若該戶居民8月份用水8噸,則該用戶8月應交水費 元;若該戶居民9月份應交水費26元,則該用戶9月份用水量為 噸;
(2)若該戶居民10月份應交水費30元,求該用戶10月份用水量;
(3)若該戶居民11月、12月共用水18噸,共交水費52元,求11月、12月各應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某制筆企業欲將200件產品運往![]() ,
,![]() ,
,![]() 三地銷售,要求運往
三地銷售,要求運往![]() 地的件數是運往
地的件數是運往![]() 地件數的2倍,各地的運費如圖所示.設安排
地件數的2倍,各地的運費如圖所示.設安排![]() 件產品運往
件產品運往![]() 地.
地.
|
|
| |
產品件數(件) |
|
| |
運費(元) |
|
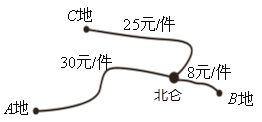
(1)①根據信息補全上表空格.②若設總運費為![]() 元,寫出
元,寫出![]() 關于
關于![]() 的函數關系式及自變量的取值范圍.
的函數關系式及自變量的取值范圍.
(2)若運往![]() 地的產品數量不超過運往
地的產品數量不超過運往![]() 地的數量,應怎樣安排
地的數量,應怎樣安排![]() ,
,![]() ,
,![]() 三地的運送數量才能達到運費最少.
三地的運送數量才能達到運費最少.
查看答案和解析>>
科目:初中數學 來源: 題型:
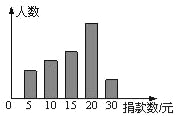
【題目】某校學生會干部對校學生會倡導的“助殘”自愿捐款活動進行抽樣調查,得到一組學生捐款情況的數據,下圖是根據這組數據繪制的統計圖,圖中從左到右各長方形高度之比為3:4:5:8:2,又知此次調查中捐20元的人數為24人,
(1)他們一共抽查了多少人?捐款數不少于20元的概率是多少?
(2)這組數據的眾數是 (元)、中位數是 (元);
(3)若該校共有660名學生,請估算全校學生共捐款多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上點A表示的數為6,B是數軸上在左側的一點,且A,B兩點間的距離為10。動點P從點A出發,以每秒6個單位長度的度沿數軸向左勻速運動,設運動時間為t![]() 秒。
秒。
![]()
(1)數軸上點B表示的數是______;當點P運動到AB的中點時,它所表示的數是_____。
(2)動點Q從點B出發,以每秒2個單位長度的速度沿數軸向左勻速運動,若點P、Q同時出發,求:
①當點P運動多少秒時,點P追上點Q?
②當點P運動多少秒時,點P與點Q間的距離為8個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】網格是由邊長為1的小正方形組成,點A,B,C位置如圖所示,若點![]() ,
,![]() .
.

(1)建立適當的平面直角坐標系,并寫出點C坐標(______,______);點B到x軸的距離是______,點C到y軸的距離是______;
(2)在平面直角坐標系中找一點D,使A,B,C,D為頂點的四邊形的所有內角都相等,再畫出四邊形ABCD.
(3)請你說出線段AB經過怎樣的變換得到線段DC的?
查看答案和解析>>
科目:初中數學 來源: 題型:
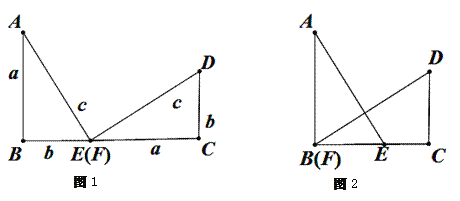
【題目】(1)以a,b為直角邊,c為斜邊作兩個全等的Rt△ABE與Rt△FCD拼成如圖1所示的圖形,使B,E,F,C四點在一條直線上(此時E,F重合),可知△ABE ≌△FCD,AE![]() DF,請你證明:
DF,請你證明:![]() ;
;
(2)在(1)中,固定△FCD,再將△ABE沿著BC平移到如圖2的位置(此時B,F重合),請你重新證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com