
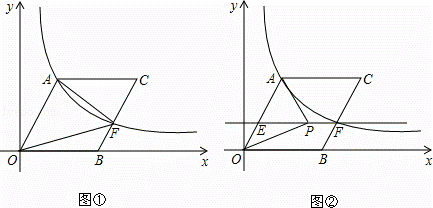
如圖①,O為坐標原點,點B在x軸的正半軸上,四邊形OACB是平行四邊形,sin∠AOB=,反比例函數y=(k>0)在第一象限內的圖象經過點A,與BC交于點F.
(1)若OA=10,求反比例函數解析式;
(2)若點F為BC的中點,且△AOF的面積S=12,求OA的長和點C的坐標;
(3)在(2)中的條件下,過點F作EF∥OB,交OA于點E(如圖②),點P為直線EF上的一個動點,連接PA,PO.是否存在這樣的點P,使以P、O、A為頂點的三角形是直角三角形?若存在,請直接寫出所有點P的坐標;若不存在,請說明理由.
考點:
反比例函數綜合題.
分析:
(1)先過點A作AH⊥OB,根據sin∠AOB=,OA=10,求出AH和OH的值,從而得出A點坐標,再把它代入反比例函數中,求出k的值,即可求出反比例函數的解析式;
(2)先設OA=a(a>0),過點F作FM⊥x軸于M,根據sin∠AOB=,得出AH=a,OH=a,求出S△AOH的值,根據S△AOF=12,求出平行四邊形AOBC的面積,根據F為BC的中點,求出S△OBF=6,
根據BF=a,∠FBM=∠AOB,得出S△BMF=BM•FM,S△FOM=6+![]() a2,再根據點A,F都在y=的圖象上,S△AOH=k,求出a,最后根據S平行四邊形AOBC=OB•AH,得出OB=AC=3
a2,再根據點A,F都在y=的圖象上,S△AOH=k,求出a,最后根據S平行四邊形AOBC=OB•AH,得出OB=AC=3![]() ,即可求出點C的坐標;
,即可求出點C的坐標;
(3)分別根據當∠APO=90°時,在OA的兩側各有一點P,得出P1,P2;當∠PAO=90°時,求出P3;當∠POA=90°時,求出P4即可.
解答:
解:(1)過點A作AH⊥OB于H,
∵sin∠AOB=,OA=10,
∴AH=8,OH=6,
∴A點坐標為(6,8),根據題意得:
8=,可得:k=48,
∴反比例函數解析式:y=![]() (x>0);
(x>0);
(2)設OA=a(a>0),過點F作FM⊥x軸于M,
∵sin∠AOB=,
∴AH=a,OH=a,
∴S△AOH=•aa=![]() a2,
a2,
∵S△AOF=12,
∴S平行四邊形AOBC=24,
∵F為BC的中點,
∴S△OBF=6,
∵BF=a,∠FBM=∠AOB,
∴FM=a,BM=![]() a,
a,
∴S△BMF=BM•FM=![]() a•
a•![]() a=
a=![]() a2,
a2,
∴S△FOM=S△OBF+S△BMF=6+![]() a2,
a2,
∵點A,F都在y=的圖象上,
∴S△AOH=k,
∴![]() a2=6+
a2=6+![]() a2,
a2,
∴a=![]()
![]() ,
,
∴OA=![]()
![]() ,
,
∴AH=![]() ,OH=2
,OH=2![]() ,
,
∵S平行四邊形AOBC=OB•AH=24,
∴OB=AC=3![]() ,
,
∴C(5![]() ,
, ![]() );
);
(3)存在三種情況:
當∠APO=90°時,在OA的兩側各有一點P,分別為:P1(![]() ,
, ![]() ),P2(﹣
),P2(﹣![]() ,
, ![]() ),
),
當∠PAO=90°時,P3(![]()
![]() ,
, ![]() ),
),
當∠POA=90°時,P4(﹣![]()
![]() ,
, ![]() ).
).

點評:
此題考查了反比例函數的綜合,用到的知識點是三角函數、平行四邊形、反比例函數、三角形的面積等,要注意運用數形結合的思想,要注意(3)有三種情況,不要漏解.


科目:初中數學 來源: 題型:
 如圖,點O為坐標原點,點A(2n,0)在x軸正半軸,將點A繞點O逆時針旋轉60°得到點B,作△OAB,點P是△OAB的重心.將點P繞坐標原點逆時針旋轉90°得到點P′,則點P′的坐標是
如圖,點O為坐標原點,點A(2n,0)在x軸正半軸,將點A繞點O逆時針旋轉60°得到點B,作△OAB,點P是△OAB的重心.將點P繞坐標原點逆時針旋轉90°得到點P′,則點P′的坐標是查看答案和解析>>
科目:初中數學 來源: 題型:
 14、如圖,以O為坐標原點,OB、OA分別在x軸、y軸上,點A的坐標為(0,3),點B坐標為(3,0),將△AOB沿AB折疊,點O落在點C處,則點C的坐標是
14、如圖,以O為坐標原點,OB、OA分別在x軸、y軸上,點A的坐標為(0,3),點B坐標為(3,0),將△AOB沿AB折疊,點O落在點C處,則點C的坐標是查看答案和解析>>
科目:初中數學 來源: 題型:
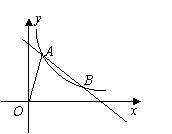
如圖所示,![]() 為坐標原點,一次函數的圖像
為坐標原點,一次函數的圖像![]() 與反比例函數
與反比例函數![]() 的圖像交于點
的圖像交于點![]()
![]()
![]() 和點
和點![]()
![]() .
.
(1)求![]() 的值和反比例函數的解析式及自變量的取值范圍;
的值和反比例函數的解析式及自變量的取值范圍;
(2)根據圖像判斷,當不等式![]() ≥
≥![]() 成立時,x的取值范圍是什么?(3)連接OB,求△OAB的面積。
成立時,x的取值范圍是什么?(3)連接OB,求△OAB的面積。
 |
查看答案和解析>>
科目:初中數學 來源:2008年初中畢業升學考試(內蒙古呼和浩特卷)數學(帶解析) 題型:解答題
如圖,已知 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,
, 的半徑為1,過
的半徑為1,過 作直線
作直線 平行于
平行于 軸,點
軸,點 在
在 上運動.
上運動.
(1)當點 運動到圓上時,求線段
運動到圓上時,求線段 的長.
的長.
(2)當點 的坐標為
的坐標為 時,試判斷直線
時,試判斷直線 與
與 的位置關系,并說明理由.
的位置關系,并說明理由.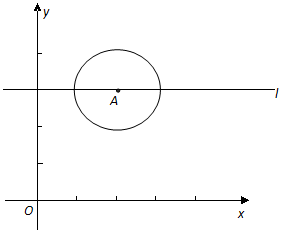
查看答案和解析>>
科目:初中數學 來源:2008年初中畢業升學考試(內蒙古呼和浩特卷)數學(解析版) 題型:解答題
如圖,已知 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,
, 的半徑為1,過
的半徑為1,過 作直線
作直線 平行于
平行于 軸,點
軸,點 在
在 上運動.
上運動.
(1)當點 運動到圓上時,求線段
運動到圓上時,求線段 的長.
的長.
(2)當點 的坐標為
的坐標為 時,試判斷直線
時,試判斷直線 與
與 的位置關系,并說明理由.
的位置關系,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com