
【題目】如圖,邊長為2![]() 的正方形ABCD中,P是對角線AC上的一個動點(點P與A、C不重合),連接BP,將BP繞點B順時針旋轉90°到BQ;連接PQ,PQ與BC交于點E,QP延長線與AD(或AD延長線)交于點F,連接CQ.求證:
的正方形ABCD中,P是對角線AC上的一個動點(點P與A、C不重合),連接BP,將BP繞點B順時針旋轉90°到BQ;連接PQ,PQ與BC交于點E,QP延長線與AD(或AD延長線)交于點F,連接CQ.求證:
(1)CQ=AP;
(2)△APB∽△CEP.

【答案】(1)見解析;(2)見解析
【解析】試題分析:(1)由題意可知AB=BC,∠ABP=∠CBQ,BP=BQ,利用“SAS”證明△ABP≌△CBQ,根據全等三角形的性質即可證明;
(2)由正方形的性質得∠BAC=∠BCA=45°,從而∠APB+∠ABP=135°.由旋轉的性質△PBQ是等腰直角三角形,從而∠APB+∠CPQ=135°,由等量代換可得∠CPQ=∠ABP,進而可證△APB∽△CEP.
證明:(1)如圖,∵線段BP繞點B順時針旋轉90°得到線段BQ,
∴BP=BQ,∠PBQ=90°.
∵四邊形ABCD是正方形,
∴BA=BC,∠ABC=90°.
∴∠ABC=∠PBQ.
∴∠ABC﹣∠PBC=∠PBQ﹣∠PBC,即∠ABP=∠CBQ.
在△BAP和△BCQ中,
∵ ,
,
∴△BAP≌△BCQ(SAS).
∴CQ=AP;
(2)如圖,∵四邊形ABCD是正方形,
∴∠BAC=![]() ∠BAD=45°,∠BCA=
∠BAD=45°,∠BCA=![]() ∠BCD=45°,
∠BCD=45°,
∴∠APB+∠ABP=180°﹣45°=135°,
∵△PBQ是等腰直角三角形,
∴∠BPQ=45°,
∴∠APB+∠CPQ=180°﹣45°=135°,
∴∠CPQ=∠ABP,
∵∠BAC=∠ACB=45°,
∴△APB∽△CEP.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:初中數學 來源: 題型:
【題目】如圖兩摞規格完全相同的課本整齊地疊放在講臺上請根據圖中所給出的數據信息,回答下列問題:

(1)每本課本的厚度為 cm.
(2)若有一摞上述規格的課本x本整齊地疊放在講臺上請用含x的代數式表示出這摞課本的頂部距離地面的高度;
(3)當x=42時,求課本的頂部距離地面的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:若A﹣B=1,則稱A與B是關于1的單位數.
(1)3與______是關于1的單位數,x﹣3與______是關于1的單位數.(填一個含x的式子)
(2)若A=3x(x+2)﹣1,![]() ,判斷A與B是否是關于1的單位數,并說明理由.
,判斷A與B是否是關于1的單位數,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
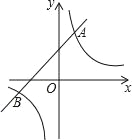
【題目】如圖,一次函數y1=kx+b(k≠0)與反比例函數y2=![]() (m≠0)相交于A和B兩點.且A點坐標為(1,3),B點的橫坐標為﹣3.
(m≠0)相交于A和B兩點.且A點坐標為(1,3),B點的橫坐標為﹣3.
(1)求反比例函數和一次函數的解析式;
(2)根據圖象直接寫出使得y1≤y2時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一條光纖線路從A地到B地需要經過C地,圖中AC=40千米,∠CAB=30°,∠CBA=45°,求AB的距離.(![]() ≈1.41,
≈1.41, ![]() ≈1.73,結果取整數)
≈1.73,結果取整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,已知,在△ABC中,∠ACB=90°,CD⊥AB垂足為D,BC=6,AC=8,求AB與CD的長.

(2)如圖,用3個全等的菱形構成活動衣帽架,頂點A、E、F、C、G、H是上、下兩排掛鉤,根據需要可以改變掛鉤之間的距離(比如AC兩點可以自由上下活動),若菱形的邊長為13厘米,要使兩排掛鉤之間的距離為24厘米,并在點B、M處固定,則B、M之間的距離是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在菱形ABCD中,點E,O,F分別為AB,AC,AD的中點,連接CE,CF,OE,OF.
(1)求證:△BCE≌△DCF;
(2)當AB與BC滿足什么關系時,四邊形AEOF是正方形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小學時候大家喜歡玩的幻方游戲,老師稍加創新改成了“幻圓”游戲,現在將﹣1、2、﹣3、4、﹣5、6、﹣7、8分別填入圖中的圓圈內,使橫、豎以及內外兩圈上的4個數字之和都相等,老師已經幫助同學們完成了部分填空,則圖中a+b的值為( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com