
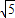 個單位每秒速度向點C運動,當一點停止運動,另一點也隨之停止,設△CPQ的面積為S,兩點同時運動,運動的時間為t秒,求S與t之間關系式,并寫出自變量取值范圍.
個單位每秒速度向點C運動,當一點停止運動,另一點也隨之停止,設△CPQ的面積為S,兩點同時運動,運動的時間為t秒,求S與t之間關系式,并寫出自變量取值范圍.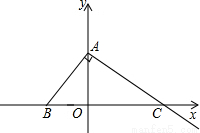
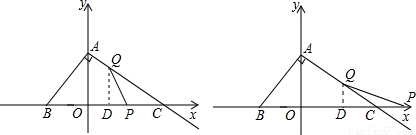 解:(1)∵AC⊥AB,
解:(1)∵AC⊥AB,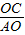 =
=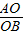
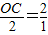 ,
, )過點Q作QD⊥BC于D,
)過點Q作QD⊥BC于D,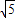 -
-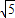 t,CP=5-4t,
t,CP=5-4t, CP•QD=
CP•QD= (5-4t)(2-t),
(5-4t)(2-t),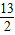 t+5(0<t<
t+5(0<t< );
); <t<2),過點Q作QD⊥BC于D,
<t<2),過點Q作QD⊥BC于D,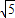 -
-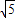 t,CP=4t-5,
t,CP=4t-5, CP•QD=
CP•QD= (4t-5)(2-t),
(4t-5)(2-t),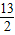 t-5(
t-5( <t<2),
<t<2), 或t=2時C、P、Q都在同一直線上,S=0.
或t=2時C、P、Q都在同一直線上,S=0.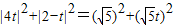 ,
,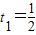 ,
,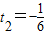 (不合題意,舍去)
(不合題意,舍去) 時,點P在圓G上.
時,點P在圓G上.

科目:初中數學 來源: 題型:
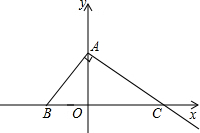 (2013•橋東區二模)如圖,Rt△ABC在平面直角坐標系中,BC在x軸上,B(-1,0)、A(0,2),AC⊥AB.
(2013•橋東區二模)如圖,Rt△ABC在平面直角坐標系中,BC在x軸上,B(-1,0)、A(0,2),AC⊥AB.| 5 |
查看答案和解析>>
科目:初中數學 來源:2012屆河北省保定市易縣九年級第一次模擬檢測數學試卷(帶解析) 題型:解答題
如圖,Rt△ABC在平面直角坐標系中,BC在x軸上,B (-1,0)、A (0,2),AC⊥AB.
(1)求線段OC的長;
(2)點P從B點出發以每秒4個單位的速度沿x軸正半軸運動,點Q從A點出發沿線段AC以每秒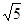 個單位的速度向點C運 動,當一點停止運動,另一點也隨之停止,設△CPQ的面 積為S,兩點同時運動,運動的時間為t秒,求S與t之間關系式,并寫出自變量取值范圍;
個單位的速度向點C運 動,當一點停止運動,另一點也隨之停止,設△CPQ的面 積為S,兩點同時運動,運動的時間為t秒,求S與t之間關系式,并寫出自變量取值范圍;
(3)Q點沿射線AC按原速度運動,⊙G過A、B、Q三點,是否有這樣的t值使點P在⊙G上、如果有求t值,如果沒有說明理由.
查看答案和解析>>
科目:初中數學 來源:2010年高級中等學校招生全國統一考試數學卷(四川南充) 題型:填空題
如圖,Rt△ABC在第一象限, ,AB=AC=2,點A在直線
,AB=AC=2,點A在直線 上,其中點A的橫坐標為1,且AB∥
上,其中點A的橫坐標為1,且AB∥ 軸,AC∥
軸,AC∥ 軸,若雙曲線
軸,若雙曲線
 與△
與△ 有交點,則k的取值范圍是 .
有交點,則k的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源:2011-2012學年河北省保定市易縣九年級第一次模擬檢測數學試卷(解析版) 題型:解答題
如圖,Rt△ABC在平面直角坐標系中,BC在x軸上,B (-1,0)、A (0,2),AC⊥AB.

(1)求線段OC的長;
(2)點P從B點出發以每秒4個單位的速度沿x軸正半軸運動,點Q從A點出發沿線段AC以每秒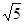 個單位的速度向點C運 動,當一點停止運動,另一點也隨之停止,設△CPQ的面
積為S,兩點同時運動,運動的時間為t秒,求S與t之間關系式,并寫出自變量取值范圍;
個單位的速度向點C運 動,當一點停止運動,另一點也隨之停止,設△CPQ的面
積為S,兩點同時運動,運動的時間為t秒,求S與t之間關系式,并寫出自變量取值范圍;
(3)Q點沿射線AC按原速度運動,⊙G過A、B、Q三點,是否有這樣的t值使點P在⊙G上、如果有求t值,如果沒有說明理由.
查看答案和解析>>
科目:初中數學 來源:2010年高級中等學校招生全國統一考試數學卷(湖北荊門) 題型:填空題
如圖,Rt△ABC在第一象限, ,AB=AC=2,點A在直線
,AB=AC=2,點A在直線 上,其中點A的橫坐標為1,且AB∥
上,其中點A的橫坐標為1,且AB∥ 軸,AC∥
軸,AC∥ 軸,若雙曲線
軸,若雙曲線
 與△
與△ 有交點,則k的取值范圍是
.
有交點,則k的取值范圍是
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com