
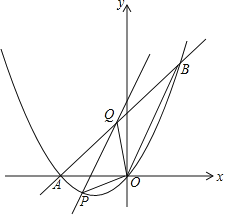
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與x軸交于原點及點A,且經過點B(4,8),對稱軸為直線x=﹣2.
(1)求拋物線的解析式;
(2)設直線y=kx+4與拋物線兩交點的橫坐標分別為x1,x2(x1<x2),當![]() 時,求k的值;
時,求k的值;
(3)連接OB,點P為x軸下方拋物線上一動點,過點P作OB的平行線交直線AB于點Q,當S△POQ:S△BOQ=1:2時,求出點P的坐標.
(坐標平面內兩點M(x1,y1),N(x2,y2)之間的距離MN=![]() )
)
【答案】(1)拋物線解析式為y=![]() x2+x;(2)k=1;(3)P(﹣2
x2+x;(2)k=1;(3)P(﹣2![]() ,﹣2
,﹣2![]() +2).
+2).
【解析】(1)先利用對稱軸公式得出b=4a,進而利用待定系數法即可得出結論;
(2)先利用根與系數的關系得出,x1+x2=4(k﹣1),x1x2=﹣16,轉化已知條件,代入即可得出結論;
(3)先判斷出OB=2PQ,進而判斷出點C是OB中點,再求出AB解析式,判斷出PC∥AB,即可得出PC解析式,和拋物線解析式聯立解方程組即可得出結論.
(1)根據題意得,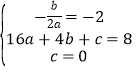 ,
,
∴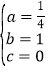 ,
,
∴拋物線解析式為y=![]() x2+x;
x2+x;
(2)∵直線y=kx+4與拋物線兩交點的橫坐標分別為x1,x2,
∴![]() x2+x=kx+4,
x2+x=kx+4,
∴x2﹣4(k﹣1)x﹣16=0,
根據根與系數的關系得,x1+x2=4(k﹣1),x1x2=﹣16,
∵![]() ,
,
∴2(x1﹣x2)=x1x2,
∴4(x1﹣x2)2=(x1x2)2,
∴4[(x1+x2)2﹣4x1x2]=(x1x2)2,
∴4[16(k﹣1)2+64]=162,
∴k=1;
(3)如圖,取OB的中點C,
∴BC=![]() OB,
OB,
∵B(4,8),
∴C(2,4),
∵PQ∥OB,
∴點O到PQ的距離等于點O到OB的距離,
∵S△POQ:S△BOQ=1:2,
∴OB=2PQ,
∴PQ=BC,∵PQ∥OB,
∴四邊形BCPQ是平行四邊形,
∴PC∥AB,
∵拋物線的解析式為y=![]() x2+x①,
x2+x①,
令y=0,
∴![]() x2+x=0,
x2+x=0,
∴x=0或x=﹣4,
∴A(﹣4,0),
∵B(4,8),
∴直線AB解析式為y=x+4,設直線PC的解析式為y=x+m,
∵C(2,4),
∴直線PC的解析式為y=x+2②,
聯立①②解得,![]() (舍)或
(舍)或![]() ,
,
∴P(﹣2![]() ,﹣2
,﹣2![]() +2).
+2).


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
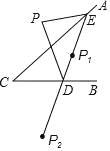
【題目】如圖,點P是直線AC外的一點,點D,E分別是AC,CB兩邊上的點,點P關于CA的對稱點P1恰好落在線段ED上,P點關于CB的對稱點P2落在ED的延長線上,若PE=2.5,PD=3,ED=4,則線段P1P2的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將數1個1,2個![]() ,3個
,3個![]() ,…,n個
,…,n個![]() (n為正整數)順次排成一列:1,
(n為正整數)順次排成一列:1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,記a1=1,a2=
,…,記a1=1,a2=![]() ,a3=
,a3=![]() ,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,則S2018=_____.
,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,則S2018=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,點C、D、E三點在同一直線上,連接BD.
(1)求證:△BAD≌△CAE;
(2)請判斷BD、CE有何大小、位置關系,并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知蝸牛從![]() 點出發,在一條數軸上來回爬行,規定:向正半軸運動記作“+”,向負半軸運動記作“-”,從開始到結束爬行的各段路程(單位:
點出發,在一條數軸上來回爬行,規定:向正半軸運動記作“+”,向負半軸運動記作“-”,從開始到結束爬行的各段路程(單位:![]() )依次為:+7,-5,-10,-8,+9,-6,+12,+4.
)依次為:+7,-5,-10,-8,+9,-6,+12,+4.
(1)若![]() 點在數軸上表示的數為-3,則蝸牛停在數軸上何處,請通過計算加以說明;
點在數軸上表示的數為-3,則蝸牛停在數軸上何處,請通過計算加以說明;
(2)蝸牛在(1)題在數軸上停的位置作以下運動:第1次向左移動1個單位長度至![]() 點,第2次從
點,第2次從![]() 點向右移動2個單位長度至
點向右移動2個單位長度至![]() 點,第3次從
點,第3次從![]() 點向左移動3個單位長度至
點向左移動3個單位長度至![]() 點,第4次從
點,第4次從![]() 點向右移動4個單位長度至
點向右移動4個單位長度至![]() 點,…,依此類推.這樣第2019次移動到的點在數軸上表示的數為(請直接寫出答案).
點,…,依此類推.這樣第2019次移動到的點在數軸上表示的數為(請直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出:
我們在分析解決某些數學問題時,經常要比較兩個數或代數式的大小,而解決問題的策略一般要進行一定的轉化,其中“作差法”就是常用的方法之一,所謂“作差法”:就是通過作差、變形,并利用差的符號來確定它們的大小,要比較代數式![]() 、
、![]() 的大小,只要作出它們的差
的大小,只要作出它們的差![]() ,若
,若![]() ,則
,則![]() .若
.若![]() ,則
,則![]() .若
.若![]() ,則
,則![]() .
.
問題解決:
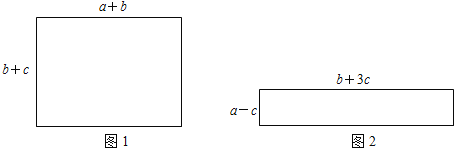
如圖,試比較圖①、圖②兩個矩形的周長![]() 、
、![]() 的大小
的大小![]() ;
;
主圖形得:![]() ;
;![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,則
,則![]() ;
;
類比應用:
(1)用材料介紹的“作差法”比較![]() 與
與![]() 的大小;
的大小;
聯系拓展:
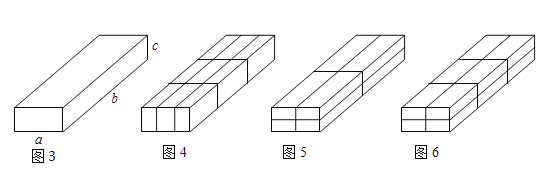
(2)小剛在超市里買了一些物品,用一個長方體的箱子“打包”,這個箱子的尺寸如圖3所示(其中![]() ),售貨員分別可按圖4、圖5、圖6三種方法進行捆綁,問哪種方法用繩最短?哪種方法用繩最長?請說明理由.
),售貨員分別可按圖4、圖5、圖6三種方法進行捆綁,問哪種方法用繩最短?哪種方法用繩最長?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵市民節約用水,某市居民生活用水按階梯式水價計費,表是該市居民“一戶一表”生活用水階梯式計費價格表的一部分信息:(水價計費=自來水銷售費用+污水處理費用)
自來水銷售價格 | 污水處理價格 | |
每戶每月用水量 | 單價:元/噸 | 單價:元/噸 |
17噸及以下 | a | 0.80 |
超過17噸不超過30噸的部分 | b | 0.80 |
超過30噸的部分 | 6.00 | 0.80 |
已知小王家2012年4月份用水20噸,交水費66元;5月份用水25噸,交水費91元.
(1)求a,b的值.
(2)小王家6月份交水費184元,則小王家6月份用水多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是等邊△ABC內一點,D是△ABC外的一點,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,連接OD.
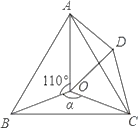
(1)求證:△OCD是等邊三角形;
(2)當α=150°時,試判斷△AOD的形狀,并說明理由;
(3)探究:當α為多少度時,△AOD是等腰三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com