
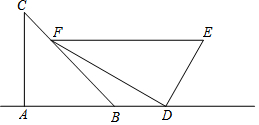
 王生是一位善于思考的學生,在一次數學活動課上,他將一副直角三角板如圖位置擺放,A、B、D在同一直線上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:
王生是一位善于思考的學生,在一次數學活動課上,他將一副直角三角板如圖位置擺放,A、B、D在同一直線上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:分析 (1)過點F作FM⊥AD于M,利用在直角三角形中,30°角所對的直角邊等于斜邊的一半和平行線的性質以及等腰直角三角形的性質即可求出BD的長.
(2)根據三角形面積公式可求△BDF的面積.
解答 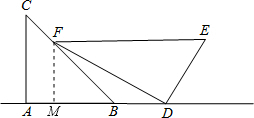 解:(1)過點F作FM⊥AD于M,
解:(1)過點F作FM⊥AD于M,
∵∠EDF=90°,∠E=60°,
∴∠EFD=30°,
∵DE=4,
∴EF=8,
∴DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=4$\sqrt{3}$,
∵EF∥AD,
∴∠FDM=30°,
∴FM=$\frac{1}{2}$DF=2$\sqrt{3}$,
∴MD=$\sqrt{F{D}^{2}-F{M}^{2}}$=6,
∵∠C=45°,
∴∠MFB=∠B=45°,
∴FM=BM=2$\sqrt{3}$,
∴BD=DM-BM=6-2$\sqrt{3}$;
(2)△BDF的面積為$\frac{1}{2}$BD•FM=$\frac{1}{2}$×(6-2$\sqrt{3}$)×2$\sqrt{3}$=6$\sqrt{3}$-6.
點評 本題考查了勾股定理的運用、平行線的性質以及等腰直角三角形的性質,解題的關鍵是作垂直構造直角三角形,利用勾股定理求出DM的長.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 購物金額(原價) | 優惠率 |
| 不超過3000元的部分 | 無優惠 |
| 超過3000元但不超過10000元部分 | 5% |
| 超過10000元的部分 | 10% |
| 付款時,還可以享受單筆消費滿2000元立減160元優惠 | |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
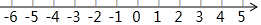 解不等式(組),并把第(2)的解集表示在數軸上.
解不等式(組),并把第(2)的解集表示在數軸上.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com