
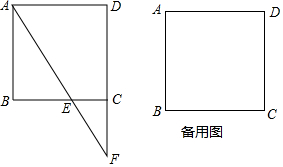
 已知邊長為3的正方形ABCD中,點E在射線BC上,且BE=2CE,連結AE交射線DC于點F,將△ABE沿直線AE翻折,點B落在點B1處.
已知邊長為3的正方形ABCD中,點E在射線BC上,且BE=2CE,連結AE交射線DC于點F,將△ABE沿直線AE翻折,點B落在點B1處.分析 (1)利用平行線性質以及線段比求出CF的值;
(2)根據平行線分線段成比例定理得到$\frac{AD}{CE}$=$\frac{DF}{FC}$,根據勾股定理和三角函數的定義即可得到結論.
解答 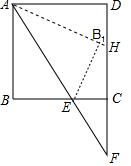 解:(1)∵AB∥DF,
解:(1)∵AB∥DF,
∴$\frac{AB}{CF}$=$\frac{BE}{CE}$,
∵BE=2CE,AB=3,
∴$\frac{3}{CF}$=$\frac{2CE}{CE}$,
∴CF=$\frac{3}{2}$;
(2)若點E在邊BC上,延長AB1交DC于H,∵∠BAE=∠B1AE=∠DFE,
∴AH=FH,AE=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
$\frac{EF}{AE}$=$\frac{CE}{BE}$=$\frac{1}{2}$,
設DH=x,CH=3-x,
∵CF=1,5,
∴AH=FH=$\frac{9}{2}$-x,
∵AD2+DH2=AH2,
∴32+x2=($\frac{9}{2}$-x)2,
∴x=$\frac{5}{4}$,
∴DH=$\frac{5}{4}$,AH=$\frac{13}{4}$,
∴sin∠DAB1=$\frac{DH}{AH}$=$\frac{5}{13}$;
若點E在邊BC的延長線上,如圖,設直線AB1與CD延長線相交于點N
同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴$\frac{AD}{CE}$=$\frac{DF}{FC}$,
∴DF=FC=$\frac{3}{2}$,
設DN=x,則AN=NF=x+$\frac{3}{2}$.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+$\frac{3}{2}$)2,
∴x=$\frac{9}{4}$.
∴DN=$\frac{9}{4}$,AN=$\frac{15}{4}$,
∴sin∠DAB1=$\frac{DN}{AN}$=$\frac{3}{5}$.
點評 本題考查正方形的性質,線段比以及勾股定理等相關知識的綜合運用,注意兩種情況的分析探討.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
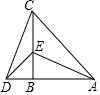 已知:如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC上,且BE=BD.
已知:如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC上,且BE=BD.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知∠CBD=∠ACB,要說明△ABC≌△DCB,
如圖,已知∠CBD=∠ACB,要說明△ABC≌△DCB,查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com