

 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)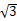 /3=3
/3=3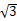 =5.1(米)
=5.1(米)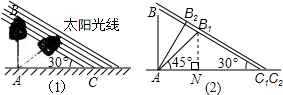
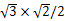 ≈3.5(米),
≈3.5(米),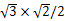 ×
×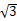 ≈6.1(米),
≈6.1(米),

科目:初中數學 來源:不詳 題型:解答題
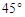 .為了方便行人推車過天橋,市政部門決定降低坡度,使新坡面的傾斜角為
.為了方便行人推車過天橋,市政部門決定降低坡度,使新坡面的傾斜角為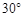 ,若新坡角下需留3米的人行道,問離原坡角10米的建筑物是否需要拆除?
,若新坡角下需留3米的人行道,問離原坡角10米的建筑物是否需要拆除?
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.1 | B.3 | C.6 | D.非以上答案 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com