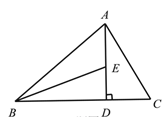
【題目】如圖，AD是△ABC邊
上的高，BE平分∠△ABC交AD于點E．若∠C=60°，∠BED=70°． 求∠ABC和∠BAC的度數．
【答案】∠ABC=40°, ∠BAC=80°
【解析】試題分析：先根據AD是△ABC的高得出∠ADB=90°，再由三角形內角和定理及三角形外角的性質可知∠DBE+∠ADB+∠BED=180°，故∠DBE=180°-∠ADB-∠BED=20°．根據BE平分
∠ABC得出∠ABC=2∠DBE=40°．根據∠BAC+∠ABC+∠C=180°，∠C=60°即可得出結論．
解：∵AD是△ABC的高，
∴∠ADB=90°，
又∵
，∠°BED=70°，
∴
．
∵BE平分∠ABC，
∴∠ABC=2∠DBE=40° ．
又∵∠BAC+∠ABC+∠C=180°，∠C=60°，
∴∠BAC=180°-∠ABC-∠C=80°．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】某地市話的收費標準為：(1)通話時間在3分鐘以內(包括3分鐘)話費0.3元；(2)通話時間超過3分鐘時，超過部分的話費按每分鐘0.11元計算．在一次通話中，如果通話時間超過3分鐘，那么話費y(元)與通話時間x(分)之間的關系式為______________．
查看答案和解析>>
科目：初中數學 來源： 題型：
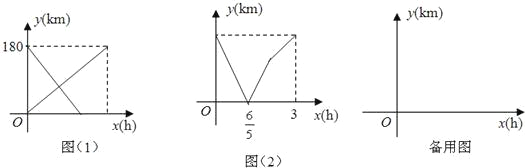
【題目】甲、乙兩車分別從A、B兩地同時相向而行，勻速開往對方所在地，圖（1）表示甲、乙兩車離A地的路程y（km）與出發時間x（h）的函數圖象，圖（2）表示甲、乙兩車間的路程y（km）與出發時間x（h）的函數圖象．
（1）A、B兩地的距離為 km，
h的實際意義是 ；
（2）求甲、乙兩車離B地的路程y（km）與出發時間x（h）的函數關系式及x的取值范圍，并畫出圖象（不用列表，圖象畫在備用圖中）；
（3）丙車在乙車出發10分鐘時從B地出發，勻速行駛，且比乙車提前20分鐘到達A地，那么，丙車追上乙車多長時間后與甲車相遇？
查看答案和解析>>
科目：初中數學 來源： 題型：
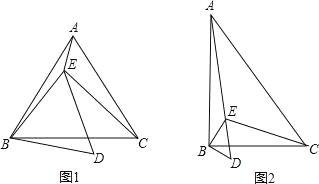
【題目】已知點E在△ABC內，∠ABC=∠EBD=α，∠ACB=∠EDB=60°，∠AEB=150°，∠BEC=90°．
（1）當α=60°時（如圖1），
①判斷△ABC的形狀，并說明理由；
②求證：BD=
AE；
（2）當α=90°時（如圖2），求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
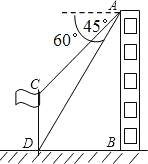
【題目】在20m高的樓AB的前方有一個旗桿CD，從樓的頂端A測得旗桿的頂端C的俯角為45°，底端D的俯角為60°．
（1）求旗桿的底端D與樓的底端B的距離；
（2）求旗桿CD的高度．
[說明：（1）（2）的計算結果精確到0.01m．參考數據：
≈1.414，
≈1.732]．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com