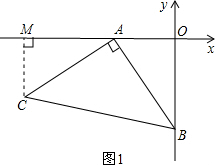
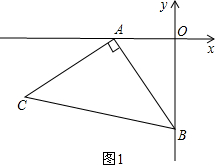
解:(1)過C作CM⊥x軸于M點,如圖1,
∵CM⊥OA,AC⊥AB,
∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°
則∠MAC=∠OBA
在△MAC和△OBA中
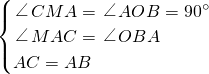
則△MAC≌△OBA(AAS)
則CM=OA=2,MA=OB=4,則點C的坐標為(-6,-2);
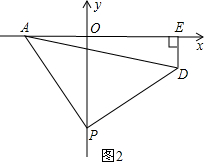
(2)過D作DQ⊥OP于Q點,如圖2,則OP-DE=PQ,∠APO+∠QPD=90°
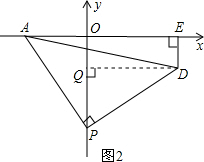
∠APO+∠OAP=90°,則∠QPD=∠OAP,
在△AOP和△PDQ中
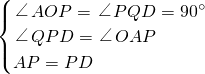
則△AOP≌△PDQ(AAS)
∴OP-DE=PQ=OA=2;
(3)結論②是正確的,m+n=-4,
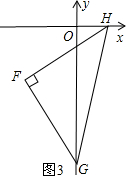
如圖3,過點F分別作FS⊥x軸于S點,FT⊥y軸于T點,
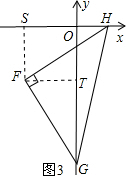
則FS=FT=2,∠FHS=∠HFT=∠FGT,
在△FSH和△FTG中
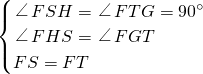
則△FSH≌△FTG(AAS)
則GT=HS,
又∵G(0,m),H(n,0),點F坐標為(-2,-2),
∴OT═OS=2,OG=|m|=-m,OH=n,
∴GT=OG-OT=-m-2,HS=OH+OS=n+2,
則-2-m=n+2,
則m+n=-4.
分析:(1)要求點C的坐標,則求C的橫坐標與縱坐標,因為AC=AB,則作CM⊥x軸,即求CM和AM的值,容易得△MAC≌△OBA,根據已知即可求得C點的值;
(2)求OP-DE的值則將其放在同一直線上,過D作DQ⊥OP于Q點,即是求PQ的值,由圖易求得△AOP≌△PDQ(AAS),即可求得PQ的長;
(3)利用(2)的結論,可知m+n為定長是正確的,過F分別作x軸和y軸的垂線,類似(2),即可求得m+n的值.
點評:本題考查了三角形全等的判定和性質;熟記三角形全等的求法,尤其是Rt△,數形結合是重要的解題方法,同學們一定要學會應用.

 解:(1)過C作CM⊥x軸于M點,如圖1,
解:(1)過C作CM⊥x軸于M點,如圖1,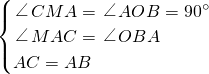

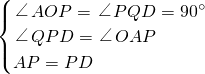

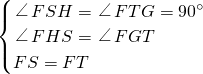


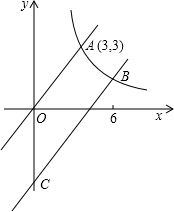 圖象交于點B(6,m)與y軸交于點C,
圖象交于點B(6,m)與y軸交于點C, 已知:如圖,射線OA和點P.
已知:如圖,射線OA和點P.