
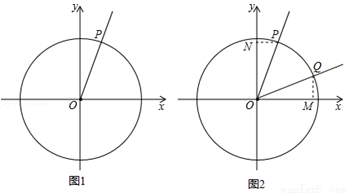
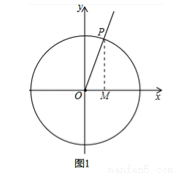
(本題滿分12分)定義:如圖1,射線OP與原點為圓心,半徑為1的圓交于點P,記∠xOP=α,則點P的橫坐標叫做角 的余弦值,記作
的余弦值,記作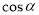 ;點P的縱坐標叫做角
;點P的縱坐標叫做角 的正弦值,記作
的正弦值,記作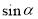 ;縱坐標與橫坐標的比值叫做角
;縱坐標與橫坐標的比值叫做角 的正切值,記作
的正切值,記作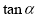 .
.
如:當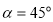 時, 點P的橫坐標為
時, 點P的橫坐標為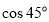 =
=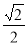 ,縱坐標為
,縱坐標為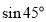 =
=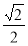 即P(
即P(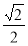 ,
,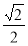 ).
).
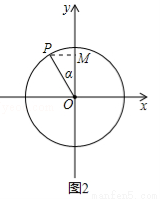
又如:在圖2中,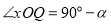 (
( 為銳角), PN
為銳角), PN
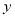 軸,QM
軸,QM
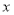 軸,易證△OQM≌△OPN, 則Q點的縱坐標
軸,易證△OQM≌△OPN, 則Q點的縱坐標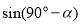 等于點P的橫坐標
等于點P的橫坐標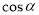 ,得
,得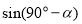 =
= 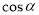 .
.
解決以下四個問題:
(1)當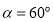 時,求點P的坐標;
時,求點P的坐標;
(2)當 是銳角時,則
是銳角時,則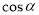 +
+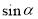 1(用>或<填空),
1(用>或<填空),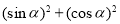 = ;
= ;
(3)求證: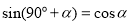 (
( 為銳角);
為銳角);
(4)求證:tan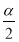 =
=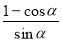 (
( 為銳角);
為銳角);
(1)(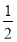 ,
,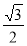 );(2)
);(2) >,1;(3)證明見試題解析;(4)證明見試題解析.
>,1;(3)證明見試題解析;(4)證明見試題解析.
【解析】
試題分析:(1)點P的橫坐標為cos60°,縱坐標為sin60°,從而可得點P的坐標;
(2)結合圖形可在△POM中,表示出cosα+sinα,繼而與半徑長1,比較即可;根據勾股定理可得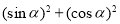 =1;
=1;
(3)畫出圖形,根據cosα及sin(90°+α)表示的實際意義,可得出結論;
(4)構造圖形,如圖,分別表示出tan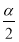 ,及
,及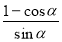 表示的線段比,繼而可得出結論.
表示的線段比,繼而可得出結論.
試題解析:(1)點P的坐標為(cos60°,sin60°)=(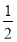 ,
,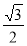 );
);
(2)如圖1所示:∠MOP=α,∵半徑為1,∴cosα=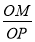 =OM,sinα=
=OM,sinα=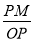 =PM,
=PM,
∴cosα+sinα=OM+PM>OP=1;
∴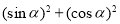 =
=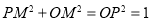 ;
;
(3)如圖2所示:∠MOP=α,點P的縱坐標為sin(90°+α),值為OM的長度,cosα=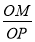 =OM,∴sin(90°+α)=cosα;
=OM,∴sin(90°+α)=cosα;
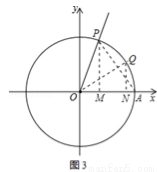
(4)如圖3所示:∠AOQ=∠POQ=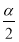 ,∠AOP=α,則cosα=
,∠AOP=α,則cosα=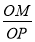 =OM,sinα=
=OM,sinα=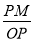 =PM,∴
=PM,∴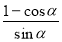 =
=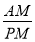 =tan∠APM,∵OQ是∠AOP的角平分線,∴OQ⊥AP,∴∠AOQ+∠OAP=90°,∵∠APM+∠OAP=90°,∴∠AOP=∠APM,即
=tan∠APM,∵OQ是∠AOP的角平分線,∴OQ⊥AP,∴∠AOQ+∠OAP=90°,∵∠APM+∠OAP=90°,∴∠AOP=∠APM,即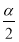 =∠APM,∴tan
=∠APM,∴tan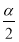 = tan∠APM =
= tan∠APM =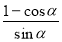 .
.
考點:圓的綜合題.


科目:初中數學 來源:2014-2015學年內蒙古赤峰市寧城縣七年級上學期期末考試數學試卷(解析版) 題型:填空題
在-5,-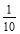 ,-3.5,-0.01,-2,-212各數中,最大的數是 .
,-3.5,-0.01,-2,-212各數中,最大的數是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省九年級上學期12月月考數學試卷(解析版) 題型:解答題
已知二次函數y=x2﹣4x+3.
(1)用配方法求其圖象的頂點C的坐標,并描述該函數的函數值隨自變量的增減而變化的情況;
(2)求函數圖象與x軸的交點A,B的坐標,及△ABC的面積.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省九年級上學期12月月考數學試卷(解析版) 題型:選擇題
如圖是二次函數y=ax2+bx+c的圖象的一部分,對稱軸是直線x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是拋物線上的兩點,則y1<y2.
上述4個判斷中,正確的是( )
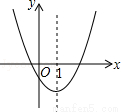
A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省九年級上學期12月月考數學試卷(解析版) 題型:選擇題
對于二次函數y=(x﹣1)2+2的圖象,下列說法正確的是( )
A.開口向 下 B.對稱軸是x=﹣1
C.頂點坐標是(1,2)D.與x軸有兩個交點
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省射陽縣九年級上學期期末考試數學試卷(解析版) 題型:解答題
(本題滿分8分)在平面直角坐標系xOy中,直線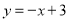 與兩坐標軸圍成一個△AOB.現將背面完全相同,正面分別標有數1、2、3、
與兩坐標軸圍成一個△AOB.現將背面完全相同,正面分別標有數1、2、3、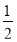 、
、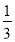 的5張卡片洗勻后,背面朝上,從中任取一張,將該卡片上的數作為點P的橫坐標,再在剩下的4張卡片中任取一張,將該卡片上的數作為點P的縱坐標,請用所學的知識求出點P落在△AOB內部(不包括邊界)的概率.
的5張卡片洗勻后,背面朝上,從中任取一張,將該卡片上的數作為點P的橫坐標,再在剩下的4張卡片中任取一張,將該卡片上的數作為點P的縱坐標,請用所學的知識求出點P落在△AOB內部(不包括邊界)的概率.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省射陽縣九年級上學期期末考試數學試卷(解析版) 題型:填空題
一山坡的的坡比為3:4,一人沿山坡向上走了20米,那么這人垂直高度上升了_ _米.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市九年級上學期第二次月考數學試卷(解析版) 題型:解答題
(本題滿分10分)沿海開發公司準備投資開發A、B兩種新產品,通過市場調研發現:
(1)若單獨投資A種產品,則所獲利潤yA(萬元)與投資金額x(萬元)之間滿足正比例函數關系:yA=kx;
(2)若單獨投資B種產品,則所獲利潤yB(萬元)與投資金額x(萬元)之間滿足二次函數關系:yB=ax2+bx.
(3)根據公司信息部的報告,yA,yB(萬元)與投資金額x(萬元)的部分對應值如下表所示:

(1)填空:yA= ;yB= ;
(2)若公司準備投資20萬元同時開發A、B兩種新產品,設公司所獲得的總利潤為W(萬元),試寫出W與某種產品的投資金額x(萬元)之間的函數關系式;
(3)請你設計一個在(2)中能獲得最大利潤的投資方案,并求出按此方案能獲得的最大利潤是多少萬元?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省婁底市九年級上學期期末模擬考試數學試卷(解析版) 題型:選擇題
某種藥品原價為36元/盒.經過連續兩次降價后售價為25元/盒.設平均每次降價的百分率為x,根據題意所列方程正確的是( )
A.36(1-x)2=36-25 B.36 (1-2x) =25
C.36(1-x)2=25 D.36(1-x2)=25
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com