
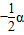 ;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.
;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.
 ;圖5,與前面步驟相同,可求得∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED,代入數據求大小.
;圖5,與前面步驟相同,可求得∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED,代入數據求大小. ,
, ,
, .
. .
. ;
; .
. 的證明如下:
的證明如下: ,
, ,
, .
. 的證明如下:
的證明如下: ,
, ,
, )=90°+
)=90°+ .
.

 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:初中數學 來源: 題型:
 22、填空或填寫理由.
22、填空或填寫理由.查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《圖形的相似》(05)(解析版) 題型:解答題
 ;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.
;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.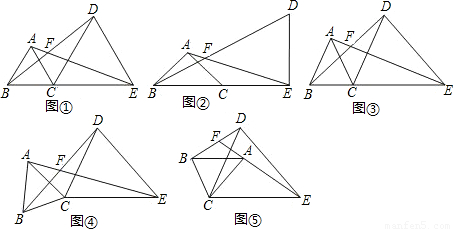
查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《圖形的旋轉》(04)(解析版) 題型:解答題
 ;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.
;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.
查看答案和解析>>
科目:初中數學 來源:2007年湖北省武漢市中考數學試卷(解析版) 題型:解答題
 ;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.
;在圖⑤中,∠AFB與∠α的數量關系是______.請你任選其中一個結論證明.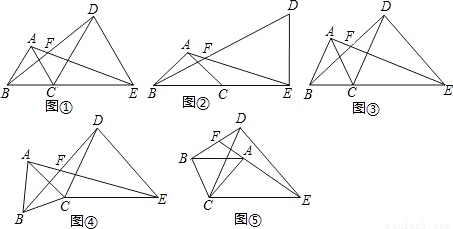
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com