
 AB,先證明△DAF∽△ABD,得到∠ADF=∠BAD=30°,再由旋轉的性質得出∠A′DB′=∠ADB=120°,根據平角的定義求出∠CDE=30°,然后由三角形外角的性質求出∠BED=120°;②如果AF=
AB,先證明△DAF∽△ABD,得到∠ADF=∠BAD=30°,再由旋轉的性質得出∠A′DB′=∠ADB=120°,根據平角的定義求出∠CDE=30°,然后由三角形外角的性質求出∠BED=120°;②如果AF= AB,先證明△DAF∽△CAB,得到∠ADF=∠ACB=90°,再由旋轉的性質得出∠BDB′=∠ADA′=90°,然后由三角形內角和定理求出∠BED=60°.
AB,先證明△DAF∽△CAB,得到∠ADF=∠ACB=90°,再由旋轉的性質得出∠BDB′=∠ADA′=90°,然后由三角形內角和定理求出∠BED=60°.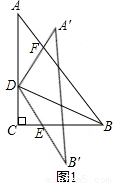 解:設線段A′D與AB邊交于點F.設AB=6a.
解:設線段A′D與AB邊交于點F.設AB=6a. AB=3a,AC=3
AB=3a,AC=3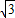 a,∠ABC=90°-∠A=60°.
a,∠ABC=90°-∠A=60°. ∠ABC=30°,
∠ABC=30°,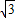 a,BD=2DC=2
a,BD=2DC=2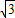 a,
a,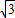 a-
a-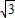 a=2
a=2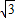 a.
a. AB時,則AF=2a.
AB時,則AF=2a.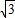 a,AB=6a,AF=2a,BD=2
a,AB=6a,AF=2a,BD=2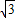 a,
a,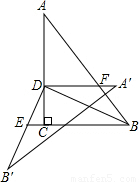 ∴∠BED=∠CDE+∠C=30°+90°=120°;
∴∠BED=∠CDE+∠C=30°+90°=120°; AB時,
AB時,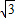 a,AC=3
a,AC=3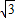 a,
a,

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 如圖,在△ABC中,AC=2,AB=3,D是AC上一點,E是AB上一點,且∠ADE=∠B,設AD=x,AE=y,則y與x之間的函數關系式是( )
如圖,在△ABC中,AC=2,AB=3,D是AC上一點,E是AB上一點,且∠ADE=∠B,設AD=x,AE=y,則y與x之間的函數關系式是( )A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在△ABC中,AB=8,AC=6,BC=7,點D在AC上,AD=2,
如圖,在△ABC中,AB=8,AC=6,BC=7,點D在AC上,AD=2,查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com