當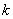
滿足條件
時，關于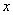
的一元二次方程
是否存在實數根
，若存在求出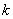值，若不存在請說明理由.
閱讀快車系列答案科目：初中數學 來源： 題型：
如圖，拋物線y= a（x﹣1）2+c與x軸交于點A（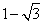
，0）和點B，將拋物線沿x軸向上翻折，頂點P落在點P/（1，3）處．過點P/作x軸的平行線交拋物線于C、D兩點，則翻折后的圖案的高與寬的比為__________（結果可保留根號）.
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，在邊長為8的正方形ABCD中，點O為AD上一動點（4＜OA＜8），以O為圓心，OA的長為半徑的圓交邊CD于點M，連接OM，過點M作⊙O的切線交邊BC于N．
（1）圖中是否存在與△ODM相似的三角形，若存在，請找出并給于證明。
（2）設DM = x，OA=R，求R關于x 的函數關系式；是否存在整數R,使得正方形ABCD內部的扇形OAM圍成的圓錐地面周長為
p ，若存在請求出此時DM的長；不存在，請說明理由。
（3）在動點O逐漸向點D運動（OA逐漸增大）的過程中，△CMN的周長如何變化？說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，將矩形ABCD沿對角線BD折疊，使C落在C′處，BC′交AD于點E，則下到結論不一定成立的是 ( )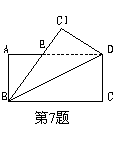
A、AD=BC′ B、∠EBD=∠EDB
C、△ABE∽△CBD D、Cos∠AEB =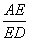
查看答案和解析>>
科目：初中數學 來源： 題型：
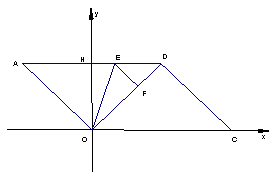
如圖，在直角坐標系中，平行四邊形AOCD的邊OC在x軸上，邊AD與y軸交與點H，CD=10，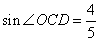
。點E、F分別是邊AD和對角線OD上的動點（點E不與A、D重合），
∠OEF=∠A=∠DOC，設AE=t,OF=s。
(1) 求直線DC的解析式；
(2) 求s關于t的函數關系式，并寫出t的取值范圍；
(3) 點E在邊AD上移動的過程中，△OEF是否有可能成為一個等腰三角形？若有可能，請求出t的值，若不可能，請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
…………3分
的根， 當兩圓相內切時，⊙O1與⊙O2的圓心距為（ ）
與
的圖象交點的橫坐標分別為a,b，則
的值為