某果園有100棵橙子樹,每一棵樹平均結600個橙子.現準備多種一些橙子樹以提高產量,但是如果多種樹,那么樹之間的距離和每一棵所接受的陽光就會減少.根據經驗估計,每多種一棵樹,平均每棵樹就會少結5個橙子.假設果園增種x棵橙子樹,果園橙子的總產量為y個.
(1)求果園增種橙子樹x(棵)與果園橙子總產量y(個)的函數關系式.
(2)在上述問題中,果園要種多少棵橙子樹,就可以使果園橙子的總產量為最多?
(3)增種多少棵橙子樹時,可以使果園橙子的總產量在60420個以上?從計算結果和數學的角度看,你有什么感想(不超過30字)?
解:(1)假設果園增種x棵橙子樹,那么果園共有(x+100)棵橙子樹,
∵每多種一棵樹,平均每棵樹就會少結5個橙子,
∴這時平均每棵樹就會少結5x個橙子,
則平均每棵樹結(600-5x)個橙子.
∵果園橙子的總產量為y,
∴則y=(x+100)(600-5x)
=-5x
2+100x+60000,
(2)∵y=(x+100)(600-5x)
=-5x
2+100x+60000,
∴當x=-

=-
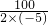
=10(棵),
y
最大=

=65000(個).
故當增種橙樹的棵數x取10棵時y的值最大,y的值最大是65000個.
(3)當y=-5x
2+100x+60000=60420時,
整理得出:x
2-20x+84=0,
(x-16)(x-4)=0,
解得:x
1=16,x
2=4,
∵拋物線對稱軸為直線x=10,
∴增種5到15棵橙子樹時,可以使果園橙子的總產量在60420個以上.
通過以上計算可以發現,果園的樹木棵數并不是越多越好,產量的多少取決于科學的計算果樹的棵數.
分析:(1)根據題意設多種x棵樹,就可求出每棵樹的產量,然后求出總產量y與x之間的關系式.
(2)利用當x=-

時,y
最大=

求出即可.
(3)根據函數關系式y=-5x
2+100x+60000=60420,結合一元二次方程解法得出即可.
點評:此題主要考查了二次函數的應用,準確分析題意,列出y與x之間的二次函數關系式是解題關鍵.

 =-
=-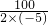 =10(棵),
=10(棵), =65000(個).
=65000(個). 時,y最大=
時,y最大= 求出即可.
求出即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案