
【題目】愛動腦筋的小明在學過用配方法解一元二次方程后,他發現二次三項式也可以配方,從而解決一些問題.
例如:![]()
![]() ;因此
;因此![]() 有最小值是1,只有當
有最小值是1,只有當![]() 時,才能得到這個式子的最小值1.
時,才能得到這個式子的最小值1.
同樣![]() ,因此
,因此![]() 有最大值是8,只有當
有最大值是8,只有當![]() 時,才能得到這個式子的最大值8.
時,才能得到這個式子的最大值8.
(1)當x= 時,代數式﹣2(x﹣3)2+5有最大值為 .
(2)當x= 時,代數式2x2+4x+3有最小值為 .
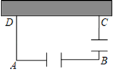
(3)矩形自行車場地ABCD一邊靠墻(墻長10m),在AB和BC邊各開一個1米寬的小門(不用木板),現有能圍成14m長的木板,當AD長為多少時,自行車場地的面積最大?最大面積是多少?
【答案】(1)3,5;(2)-1,1;(3)32.
【解析】
(1)類比例子得出答案即可;
(2)根據題意利用配方法配成(1)中的類型,進一步確定最值即可;
(3)根據題意利用長方形的面積列出式子,利用(1)(2)的方法解決問題.
解:(1)在代數式-2(x-3)2+5中,當x=3時,有最大值5,
故答案為:3、5;
(2)∵2x2+4x+3=2(x2+2x+1-1)+3=2(x+1)2+1,
∴當x=-1時,代數式2x2+4x+3有最小值為1,
故答案為:-1、1;
(3)設AD=x,則AB=14-(x+x-1)+1=16-2x,
∵S=x(16-2x)=-2(x-4)2+32,
∴當AD=4m時,面積最大值為32m2.


科目:初中數學 來源: 題型:
【題目】為落實國務院房地產調控政策,使“居者有其屋”.某市加快了廉租房的建設力度,2013年市政府共投資3億元人民幣建設了廉租房12萬平方米,2015年投資6.75億元人民幣建設廉租房,若在這兩年內每年投資的增長率相同.
(1)求每年市政府投資的增長率;
(2)若這兩年內的建設成本不變,問2015年建設了多少萬平方米廉租房?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線y=(m-1)x2+mx+m2-4的圖象經過原點,且開口向上.
(1)確定![]() 的值;
的值;
(2)求此拋物線的頂點坐標;
(3)畫出拋物線的圖象,結合圖象回答:當![]() 取什么值時,
取什么值時,![]() 隨
隨![]() 的增大而增大?
的增大而增大?
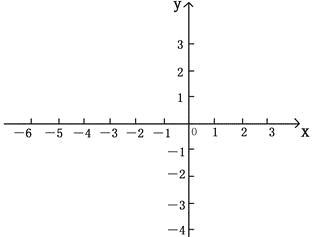
(4)結合圖象直接回答:當![]() 取什么值時,
取什么值時,![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三個盒子中分別裝有除顏色外都相同的小球,甲盒中裝有兩個球,分別為一個紅球和一個綠球;乙盒中裝有三個球,分別為兩個綠球和一個紅球;丙盒中裝有兩個球,分別為一個紅球和一個綠球,從三個盒子中各隨機取出一個小球
(1)請畫樹狀圖,列舉所有可能出現的結果
(2)請直接寫出事件“取出至少一個紅球”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
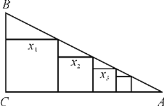
【題目】如圖所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把邊長分別為![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的n
的n![]() 個正方形依次放入△ABC中,則第n個正方形的邊長
個正方形依次放入△ABC中,則第n個正方形的邊長![]() _______________(用含n的式子表示).
_______________(用含n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠準備生產甲、乙兩種商品共8萬件銷往“一帶一路”沿線國家和地區,已知2件甲種商品與3件乙種商品的銷售額相同,3件甲種商品比2件乙種商品的銷售額多1500元.
(1)甲種商品與乙種商品的銷售單價各多少元?
(2)若甲、乙兩種商品的銷售總額不低于5400萬元,則至少銷售甲種商品多少萬件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,完成相應學習任務
旋轉對稱
把正n邊形繞著它的中心旋轉![]() 的整數倍后所得的正n邊形重合.我們說,正n邊形關于其中心有
的整數倍后所得的正n邊形重合.我們說,正n邊形關于其中心有![]() 的旋轉對稱.一般地,如果一個圖形繞著某點O旋轉角α(0<α<360°)后所得到的圖形與原圖形重合,則稱此圖形關于點O有角α的旋轉對稱.圖1就是具有旋轉對稱性質的一些圖形.
的旋轉對稱.一般地,如果一個圖形繞著某點O旋轉角α(0<α<360°)后所得到的圖形與原圖形重合,則稱此圖形關于點O有角α的旋轉對稱.圖1就是具有旋轉對稱性質的一些圖形.

任務:
(1)如圖2,正六邊形關于其中心O有 的旋轉對稱,中心對稱圖形關于其對稱中心有 的旋轉對稱;
(2)圖3是利用旋轉變換設計的具有旋轉對稱性的一個圖形,將該圖形繞其中心至少旋轉 與原圖形重合;
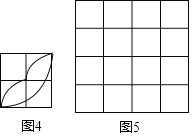
(3)請以圖4為基本圖案,在圖5中利用平移、軸對稱或旋轉進行圖案設計,使得設計出的圖案是中心對稱圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y1=x2與直線![]() 相交于A、B兩點
相交于A、B兩點
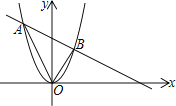
(1)求A、B兩點的坐標
(2)點O為坐標原點,△AOB的面積等于___________
(3)當y1<y2時,x的取值范圍是________________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() 的圖象過點
的圖象過點![]() 和點
和點![]() ,對稱軸為直線
,對稱軸為直線![]() .
.

![]() 求該二次函數的關系式和頂點坐標;
求該二次函數的關系式和頂點坐標;
![]() 結合圖象,解答下列問題:
結合圖象,解答下列問題:
①當![]() 時,求函數
時,求函數![]() 的取值范圍.
的取值范圍.
②當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com