
【題目】閱讀下列材料,完成相應學習任務
旋轉對稱
把正n邊形繞著它的中心旋轉![]() 的整數倍后所得的正n邊形重合.我們說,正n邊形關于其中心有
的整數倍后所得的正n邊形重合.我們說,正n邊形關于其中心有![]() 的旋轉對稱.一般地,如果一個圖形繞著某點O旋轉角α(0<α<360°)后所得到的圖形與原圖形重合,則稱此圖形關于點O有角α的旋轉對稱.圖1就是具有旋轉對稱性質的一些圖形.
的旋轉對稱.一般地,如果一個圖形繞著某點O旋轉角α(0<α<360°)后所得到的圖形與原圖形重合,則稱此圖形關于點O有角α的旋轉對稱.圖1就是具有旋轉對稱性質的一些圖形.

任務:
(1)如圖2,正六邊形關于其中心O有 的旋轉對稱,中心對稱圖形關于其對稱中心有 的旋轉對稱;
(2)圖3是利用旋轉變換設計的具有旋轉對稱性的一個圖形,將該圖形繞其中心至少旋轉 與原圖形重合;
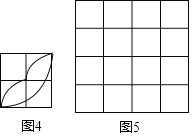
(3)請以圖4為基本圖案,在圖5中利用平移、軸對稱或旋轉進行圖案設計,使得設計出的圖案是中心對稱圖形.
【答案】(1)60°;180°;(2)72°;(3)如圖所示,是中心對稱圖形.(答案不唯一)見解析.
【解析】
(1)根據正六邊形的邊數,即可得到正六邊形關于其中心O有60°的旋轉對稱,依據中心對稱的概念,即可得到中心對稱圖形關于其對稱中心有180°的旋轉對稱;
(2)依據360°÷5=72°,即可得到將該圖形繞其中心至少旋轉72°與原圖形重合;
(3)利用平移、軸對稱或旋轉變換,即可設計出中心對稱圖形.
(1)正六邊形關于其中心O有60°的旋轉對稱,中心對稱圖形關于其對稱中心有180°的旋轉對稱;
故答案為:60°;180°;
(2)∵360°÷5=72°,
∴將該圖形繞其中心至少旋轉72°與原圖形重合;
故答案為:72°;
(3)如圖5所示,是中心對稱圖形.(答案不唯一)



科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,AD為弦,∠DBC=∠A.

(1)求證:BC是半圓O的切線;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等腰直角三角形,∠ACB=90°,D是射線CB上一點(點D不與點B重合),以AD為斜邊作等腰直角三角形ADE(點E和點C在AB的同側),連接CE.

(1)如圖①,當點D與點C重合時,直接寫出CE與AB的位置關系;
(2)如圖②,當點D與點C不重合時,(1)的結論是否仍然成立?若成立,請寫出證明過程;若不成立,請說明理由;
(3)當∠EAC=15°時,請直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】愛動腦筋的小明在學過用配方法解一元二次方程后,他發現二次三項式也可以配方,從而解決一些問題.
例如:![]()
![]() ;因此
;因此![]() 有最小值是1,只有當
有最小值是1,只有當![]() 時,才能得到這個式子的最小值1.
時,才能得到這個式子的最小值1.
同樣![]() ,因此
,因此![]() 有最大值是8,只有當
有最大值是8,只有當![]() 時,才能得到這個式子的最大值8.
時,才能得到這個式子的最大值8.
(1)當x= 時,代數式﹣2(x﹣3)2+5有最大值為 .
(2)當x= 時,代數式2x2+4x+3有最小值為 .
(3)矩形自行車場地ABCD一邊靠墻(墻長10m),在AB和BC邊各開一個1米寬的小門(不用木板),現有能圍成14m長的木板,當AD長為多少時,自行車場地的面積最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經y=ax2+bx﹣3過A(1,0)、B(3,0)、C三點.

(1)求拋物線解析式;
(2)如圖1,點P是BC上方拋物線上一點,作PQ∥y軸交BC于Q點.請問是否存在點P使得△BPQ為等腰三角形?若存在,請直接寫出P點坐標;若不存在,請說明理由;
(3)如圖2,連接AC,點D是線段AB上一點,作DE∥BC交AC于E點,連接BE.若△BDE∽△CEB,求D點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
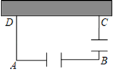
【題目】把球放在長方體紙盒內,球的一部分露出盒外,其截面如圖所示,已知EF=CD=4 cm,則球的半徑長是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC=60°,AD平分∠BAC交⊙O于點D,連接OB、OC、BD、CD.
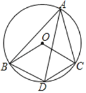
(1)求證:四邊形OBDC是菱形;
(2)當∠BAC為多少度時,四邊形OBDC是正方形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C為⊙O上一點,點P是半徑OB上一動點(不與O,B重合),過點P作射線l⊥AB,分別交弦BC,![]() 于D、E兩點,在射線l上取點F,使FC=FD.
于D、E兩點,在射線l上取點F,使FC=FD.
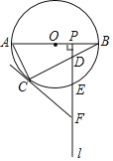
(1)求證:FC是⊙O的切線;
(2)當點E是![]() 的中點時,
的中點時,
① 若∠BAC=60°,判斷以O,B,E,C為頂點的四邊形是什么特殊四邊形,并說明理由;
② 若![]() ,且AB=20,求OP的長.
,且AB=20,求OP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
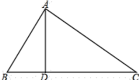
【題目】已知:如圖,![]() 中,
中,![]() 于
于![]() ,下列條件:
,下列條件:![]() ;(2)∠B=∠DAC;(3)
;(2)∠B=∠DAC;(3)![]() =
= ![]() ;(4)AB2=BD
;(4)AB2=BD![]() BC.其中一定能夠判定
BC.其中一定能夠判定![]() 是直角三角形的有( )
是直角三角形的有( )
A. 0個B. 1個C. 2個D. 3個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com