
 cm,點P為ABCDEF內的任意一點,點P到正六邊形ABCDEF各邊所在直線的距離之和為s,則s=________cm.
cm,點P為ABCDEF內的任意一點,點P到正六邊形ABCDEF各邊所在直線的距離之和為s,則s=________cm.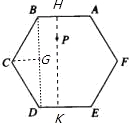 解:過P作AB的垂線,交AB、DE分別為H、K,連接BD,
解:過P作AB的垂線,交AB、DE分別為H、K,連接BD, ×
× =6,
=6,

科目:初中數學 來源: 題型:
 (2012•無錫)如圖的平面直角坐標系中有一個正六邊形ABCDEF,其中C、D的坐標分別為(1,0)和(2,0).若在無滑動的情況下,將這個六邊形沿著x軸向右滾動,則在滾動過程中,這個六邊形的頂點A、B、C、D、E、F中,會過點(45,2)的是點
(2012•無錫)如圖的平面直角坐標系中有一個正六邊形ABCDEF,其中C、D的坐標分別為(1,0)和(2,0).若在無滑動的情況下,將這個六邊形沿著x軸向右滾動,則在滾動過程中,這個六邊形的頂點A、B、C、D、E、F中,會過點(45,2)的是點查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com