
如圖,用長為20米的籬笆恰好圍成一個扇形花壇,且扇形花壇的圓心角小于180°,設扇形花壇的半徑為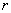 米,面積為
米,面積為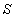 平方米.(注:
平方米.(注: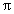 的近似值取3)
的近似值取3)
(1)求出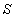 與
與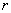 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量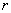 的取值范圍;
的取值范圍;
(2)當半徑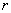 為何值時,扇形花壇的面積最大,并求面積的最大值.
為何值時,扇形花壇的面積最大,并求面積的最大值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
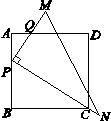
已知:如圖,Rt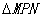 的頂點P在正方形ABCD的邊AB上,∠MPN=90°,PN經過點C,PM與AD交于點Q.
的頂點P在正方形ABCD的邊AB上,∠MPN=90°,PN經過點C,PM與AD交于點Q.
(1)在不添加字母和輔助線的情況下,圖中△APQ∽△ ;
(2)若P為AB的中點,聯結CQ,求證:AQ+BC=CQ;
(3)若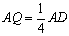 時,試探究線段PC與線段PQ的數量關系,并加以證明.
時,試探究線段PC與線段PQ的數量關系,并加以證明.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
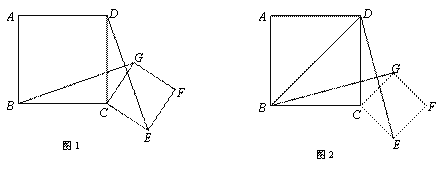
已知四邊形ABCD和四邊形CEFG都是正方形 ,且AB>CE.
(1)如圖1,連接BG、DE.求證:BG=DE;
(2)如圖2,如果正方形ABCD的邊長為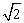 ,將正方形CEFG繞著點C旋轉到某一位置時恰好使得C
,將正方形CEFG繞著點C旋轉到某一位置時恰好使得C G//BD,BG=BD.
G//BD,BG=BD.
①求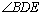 的度數;
的度數;
②請直接寫出正方形CEFG的邊長的值.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
一個袋子中裝有10個球,其中有6個黑球和4個白球,這些球除顏色外,形狀、大小、質地等完全相同,在看不到球的條件下,隨機從這個袋子中摸出一個球,摸到黑球的概率為
A.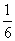 B.
B.
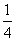 C.
C.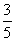 D.
D.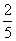

查看答案和解析>>
科目:初中數學 來源: 題型:
已知拋物線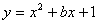 的頂點在x軸上,且與y軸交于A點. 直線
的頂點在x軸上,且與y軸交于A點. 直線 經過A、B兩點,點B的坐標為(3,4).
經過A、B兩點,點B的坐標為(3,4).
(1)求拋物線的解析式,并判斷點B是否在拋物線上;
(2)如果點B在拋物線上,P為線段AB上的一個動點(點P與A、B不重合),過P作x軸的垂線與這個二次函數的圖象交于點E,設線段PE的長為h ,點P的橫坐標為x.當x為何值時,h取得最大值,求出這時的h值.
查看答案和解析>>
科目:初中數學 來源: 題型:
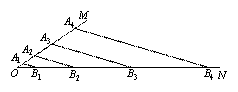
如圖,點A1、A2 、A3 、…,點B1、B2 、B3 、…,分別在射線OM、ON上,A1B1∥A2B2∥A3B3∥A4B4∥….如果A1B1=2,A1A2=2OA1,A2A3=3OA1,A3A 4=4OA1,….
那么A2B2= ,AnBn= .(n為正整數)
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com