
【題目】已知:△ABC在坐標平面內,三個頂點的坐標分別為A(0,3),B(3,4),C(2,2).(正方形網格中,每個小正方形的邊長是1個單位長度)
(1)畫出△ABC向下平移4個單位得到的△A1B1C1 , 并直接寫出C1點的坐標;
(2)以點B為位似中心,在網格中畫出△A2BC2 , 使△A2BC2與△ABC位似,且位似比為2:1,并直接寫出C2點的坐標及△A2BC2的面積.
【答案】
(1)
如圖,△A1B1C1即為所求,C1(2,﹣2)
(2)
如圖,
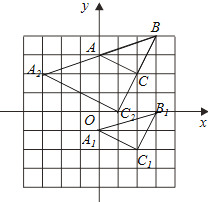
△A2BC2即為所求,C2(1,0),
△A2BC2的面積:
6×4﹣ ![]() ×2×6﹣
×2×6﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×2×4
×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
【解析】(1)根據網格結構,找出點A、B、C向下平移4個單位的對應點A1、B1、C1的位置,然后順次連接即可,再根據平面直角坐標系寫出點C1的坐標;(2)延長BA到A2 , 使AA2=AB,延長BC到C2 , 使CC2=BC,然后連接A2C2即可,再根據平面直角坐標系寫出C2點的坐標,利用△A2BC2所在的矩形的面積減去四周三個小直角三角形的面積,列式計算即可得解.
【考點精析】解答此題的關鍵在于理解作圖-位似變換的相關知識,掌握對應點到位似中心的距離比就是位似比,對應線段的比等于位似比,位似比也有順序;已知圖形的位似圖形有兩個,在位似中心的兩側各有一個.位似中心,位似比是它的兩要素.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:初中數學 來源: 題型:
【題目】在數學中,有許多關系都是在不經意間被發現的.當然,沒有敏銳的觀察力是做不到的.數學家們往往是這樣來研究問題的:特值探究–猜想歸納–邏輯證明–總結應用.下面我們也來像數學家們那樣分四步找出這兩個代數式的關系:對于代數式![]() 與
與![]() .
.
![]() 特值探究:
特值探究:
當![]() ,
,![]() 時,
時,![]() ________;
________;![]() ________
________
當![]() ,
,![]() 時,
時,![]() ________;
________;![]() ________
________
![]() 猜想歸納:
猜想歸納:
觀察![]() 的結果,寫出
的結果,寫出![]() 與
與![]() 的關系:________.
的關系:________.
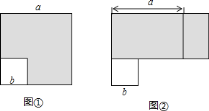
![]() 邏輯證明:如圖,邊長為
邏輯證明:如圖,邊長為![]() 的正方形紙片剪出一個邊長為
的正方形紙片剪出一個邊長為![]() 的小正方形之后,剩余部分(即陰影部分)又剪拼成一個矩形(不重疊無縫隙),請你說說是如何用這個圖來得出
的小正方形之后,剩余部分(即陰影部分)又剪拼成一個矩形(不重疊無縫隙),請你說說是如何用這個圖來得出![]() 中的關系?
中的關系?
![]() 總結應用:利用你發現的關系,求:
總結應用:利用你發現的關系,求:
①若![]() ,且
,且![]() ,則
,則![]() ________;
________;
②![]() 的值.(提示:你可能要用到公式
的值.(提示:你可能要用到公式![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線的對稱軸是直線x=2,頂點A的縱坐標為1,點B(4,0)在此拋物線上.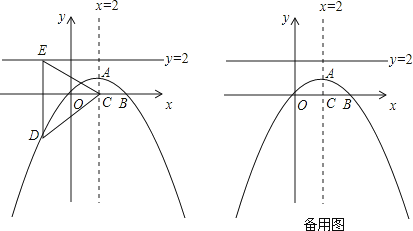
(1)求此拋物線的解析式;
(2)若此拋物線對稱軸與x軸交點為C,點D(x,y)為拋物線上一動點,過點D作直線y=2的垂線,垂足為E.
①用含y的代數式表示CD2 , 并猜想CD2與DE2之間的數量關系,請給出證明;
②在此拋物線上是否存在點D,使∠EDC=120°?如果存在,請直接寫出D點坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為4,點E、F分別在邊AB、BC上,且AE=BF=1,CE、DF交于點O.下列結論:①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④S△ODC=S四邊形BEOF中,正確的有( )
,④S△ODC=S四邊形BEOF中,正確的有( ) 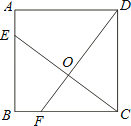
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)![]() (2)
(2)![]()
(3)(-2![]() )-(+4.7)-(-0.4)+ (-3.3) (4)
)-(+4.7)-(-0.4)+ (-3.3) (4)![]()
(5)![]() (6)(
(6)(![]() -
-![]() +
+![]() )×(-36)
)×(-36)
(7)![]() (8)—
(8)—![]() (用簡便方法計算)
(用簡便方法計算)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暴雨過后,某地遭遇山體滑坡,武警總隊派出一隊武警戰士前往搶險.半小時后,第二隊前去支援,平均速度是第一隊的1.5倍,結果兩隊同時到達.已知搶險隊的出發地與災區的距離為90千米,兩隊所行路線相同.
(1)問兩隊的平均速度分別是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為某三岔路口交通環島的簡化模型,在某高峰時刻,單位時間進出路口A,B,C的機動車輛數如圖所示.圖中x1,x2,x3分別表示該時段單位時間通過路段AB,BC,CA的機動車輛數(假設單位時間內在上述路段中同一路段上駛入與駛出的車輛數相等),則有( )

A. x1>x2>x3 B. x1>x3>x2 C. x2>x3>x1 D. x3>x2>x1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】深化理解:
新定義:對非負實數x “四舍五入”到個位的值記為![]() ,
,
即:當n為非負整數時,如果![]() ;
;
反之,當n為非負整數時,如果![]()
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
試解決下列問題:
(1)填空:①![]() =________(
=________(![]() 為圓周率); ②如果
為圓周率); ②如果![]() 的取值范圍為____________________.
的取值范圍為____________________.
(2)若關于x的不等式組 的整數解恰有3個,求a的取值范圍.
的整數解恰有3個,求a的取值范圍.
(3)求滿足![]() 的所有非負實數x的值.
的所有非負實數x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com