
【題目】如圖,拋物線的對稱軸是直線x=2,頂點A的縱坐標為1,點B(4,0)在此拋物線上.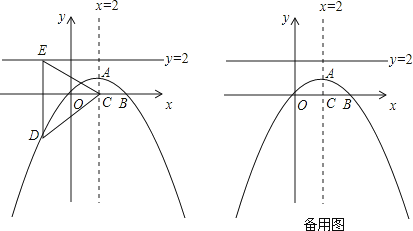
(1)求此拋物線的解析式;
(2)若此拋物線對稱軸與x軸交點為C,點D(x,y)為拋物線上一動點,過點D作直線y=2的垂線,垂足為E.
①用含y的代數式表示CD2 , 并猜想CD2與DE2之間的數量關系,請給出證明;
②在此拋物線上是否存在點D,使∠EDC=120°?如果存在,請直接寫出D點坐標;如果不存在,請說明理由.
【答案】
(1)
解:依題意,設拋物線的解析式為:y=a(x﹣2)2+1,代入B(4,0),得:
a(4﹣2)2+1=0,解得:a=﹣ ![]()
∴拋物線的解析式:y=﹣ ![]() (x﹣2)2+1
(x﹣2)2+1
(2)
解:
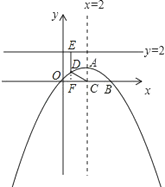
①猜想:CD2=DE2;
證明:由D(x,y)、C(2,0)、E(x,2)知:
CD2=(x﹣2)2+y2,DE2=(y﹣2)2;
由(1)知:(x﹣2)2=﹣4(y﹣1)=﹣4y+4,代入CD2中,得:
CD2=y2﹣4y+4=(y﹣2)2=DE2.
②由于∠EDC=120°>90°,所以點D必在x軸上方,且拋物線對稱軸左右兩側各有一個,以左側為例:
延長ED交x軸于F,則EF⊥x軸;
在Rt△CDF中,∠FDC=180°﹣120°=60°,∠DCF=30°,則:
CD=2DF、CF= ![]() DF;
DF;
設DF=m,則:CF= ![]() m、CD=DE=2m;
m、CD=DE=2m;
∵EF=ED+DF=2m+m=2,
∴m= ![]() ,DF=m=
,DF=m= ![]() ,CF=
,CF= ![]() m=
m= ![]() ,OF=OC﹣CF=2﹣
,OF=OC﹣CF=2﹣ ![]() ,
,
∴D(2﹣ ![]() ,
, ![]() );
);
同理,拋物線對稱軸右側有:D(2+ ![]() ,
, ![]() );
);
綜上,存在符合條件的D點,且坐標為(2﹣ ![]() ,
, ![]() )或(2+
)或(2+ ![]() ,
, ![]() ).
).
【解析】(1)已知拋物線的頂點坐標,可以將拋物線的解析式設為頂點式,再代入B點的坐標求解即可.(2)①由坐標系兩點間的距離公式不難得到CD2和DE2的表達式,再將(1)的拋物線解析式代入CD2的表達式中,用y替換掉x后,比較兩者的大小關系即可;②∠EDC是鈍角,那么點D一定在x軸的上方,且拋物線對稱軸的左右兩側各一個(它們關于拋物線對稱軸對稱),延長ED交x軸于F,在Rt△CDF中,∠DCF=30°,那么DC=2DF、CF= ![]() DF,設出DF的長后,可以表示出CD、DE的長,由EF=ED+DF=2即可得出DF的長,從而求出點D的坐標.
DF,設出DF的長后,可以表示出CD、DE的長,由EF=ED+DF=2即可得出DF的長,從而求出點D的坐標.


科目:初中數學 來源: 題型:
【題目】某班級從甲乙兩位同學中選派一人參加“秀美山河”知識競賽,老師對他們的五次模擬成績(單位:分)進行了整理,美工計算出甲成績的平均數是80,甲乙成績的方差分別是320,40,但繪制的統計圖尚不完整.
甲乙兩人模擬成績統計表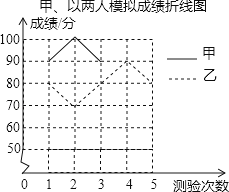
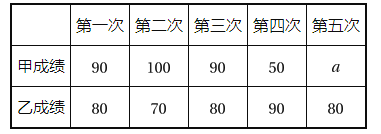
根據以上信息,請你解答下列問題:
(1)a=;
(2)請完成圖中表示甲成績變化情況的折線;
(3)求乙成績的平均數;
(4)從平均數和方差的角度分析,誰將被選中.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD的面積是16,對角線AC、BD相交于點O,點M1、N1、P1分別為線段OD、DC、CO的中點,順次連接M1N1、N1 P1、P1M1得到第一個△P1M1N1 , 面積為S1 , 分別取M1N1、N1P1、P1M1三邊的中點P2、M2、N2 , 得到第二個△P2M2N2 , 面積記為S2 , 如此繼續下去得到第n個△PnMnNn , 面積記為Sn , 則Sn﹣Sn﹣1= . (用含n的代數式表示,n≥2,n為整數)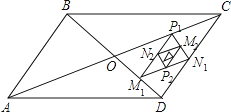
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小梅將邊長分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …長的若干個正方形按一定規律拼成不同的長方形,如圖所示.
…長的若干個正方形按一定規律拼成不同的長方形,如圖所示.
![]() 求第四個長方形的周長;
求第四個長方形的周長;
![]() 當
當![]() 時,求第五個長方形的面積.(用科學記數法表示)
時,求第五個長方形的面積.(用科學記數法表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
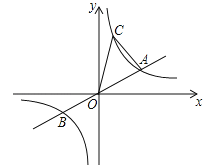
【題目】如圖,已知:直線![]() 與雙曲線
與雙曲線![]() 交于A.B兩點,且點A的橫坐標為4, 若雙曲線
交于A.B兩點,且點A的橫坐標為4, 若雙曲線![]() 上一點C的縱坐標為8,連接AC.
上一點C的縱坐標為8,連接AC.
(1)填空: k的值為_______; 點B的坐標為___________;點C的坐標為___________.
(2)直接寫出關于的不等式![]() 的解集.
的解集.
(3)求三角形AOC的面積
(4) 若在x軸上有點M,y軸上有點N,且點M.N.A.C四點恰好構成平行四邊形,直接寫出點M.N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是雙曲線y= ![]() 在第二象限分支上的任意一點,點B、點C、點D分別是點A關于x軸、坐標原點、y軸的對稱點.若四邊形ABCD的面積是8,則k的值為( )
在第二象限分支上的任意一點,點B、點C、點D分別是點A關于x軸、坐標原點、y軸的對稱點.若四邊形ABCD的面積是8,則k的值為( )
A.﹣1
B.1
C.2
D.﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC在坐標平面內,三個頂點的坐標分別為A(0,3),B(3,4),C(2,2).(正方形網格中,每個小正方形的邊長是1個單位長度)
(1)畫出△ABC向下平移4個單位得到的△A1B1C1 , 并直接寫出C1點的坐標;
(2)以點B為位似中心,在網格中畫出△A2BC2 , 使△A2BC2與△ABC位似,且位似比為2:1,并直接寫出C2點的坐標及△A2BC2的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點O是AC邊上的一個動點,過點O作直線MN∥BC,設MN交∠BCA的平分線于點E,交∠BCA的外角平分線于點F.
(1)判斷OE與OF的大小關系?并說明理由?
(2)當點O運動何處時,四邊形AECF是矩形?并說出你的理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com