
在平面直角坐標系xOy,已知拋物線y=x2-2mx+m2-9.
(1)求證:無論m為何值,該拋物線與x軸總有兩個交點;
(2)該拋物線與x軸交于A,B兩點,點A在點B的左側,且OA<OB,與y軸的交點坐標為(O,-5),求此拋物線的解析式;
(3)在(2)的條件下,拋物線的對稱軸與x軸的交點為N,若點M是線段AN上的任意一點,過點M作直線MC⊥x軸,交拋物線于點C,記點C關于拋物線對稱軸的對稱點為D,點P是線段MC上一點,且滿足MP=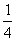 MC,連結CD,PD,作PE⊥PD交x軸與點E,問是否存在這樣的點E,使得
MC,連結CD,PD,作PE⊥PD交x軸與點E,問是否存在這樣的點E,使得 PE=PD,若存在,求出點E的坐標;若不存在,請說明理由.
PE=PD,若存在,求出點E的坐標;若不存在,請說明理由.
解:(l)△=(-2m)2 -4(m2 -9) =4m2-4m2+36 =36 >0,所以無論
m為何值,一元二次方程x2 -2mx+m2-9 =0總有兩個不相
等的實數根;
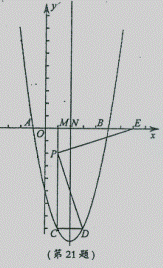 說明:指出拋物線開口向上,頂點在x軸下方,所以該 拋
說明:指出拋物線開口向上,頂點在x軸下方,所以該 拋
物線與x軸總有兩交點 (亦可)
(2) ∵拋物線y=x2-2mx+m2-9與y軸交點生標為(0,-5),
∴-5=m2-9.解得m=t2.
∵拋物線y=x2-mx+m2-9與x軸交于A,B兩點,點A在點B 的左側,且0A<OB.
∴m=2.
∴拋物線的解析式為y =x2-4x-5.
(3)假設點E存在,
∵MC⊥EM,CD⊥MC,∴∠EMP= ∠PCD.
∵ PE⊥ PD.∴∠EPM=∠PDC.
∵PE= PD.∴△EPM≌△PDC.
∴PM=DC,EM=PD.
該拋物線y=x2-4x-5的對稱軸x=2,N(2,O),A(一l,O),B(5,0)
設C(x0 ,y0),則D(4-x0,y0),P(x0, 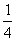 y0).(其中一l<x0<2,y0=x02-4x0-5)
y0).(其中一l<x0<2,y0=x02-4x0-5)
由CD= PM 得4 - 2xo=一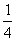 y0.
y0.
即4 - 2x0=一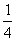 ( x02-4x0-5).
( x02-4x0-5).
解得x0=1或x0=1l(舍去)
∴M(1,O),C(1,一8) ∴P(1,一2). ∴PC =6.
∴ME= PC=6. ∴E(7,O)
∴點E存在其坐標為(7,O).


科目:初中數學 來源: 題型:
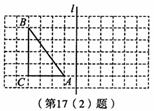
如圖,在邊長為1個單位長度的小正方形所組成的網格中,△ABC的頂點均在格點上.
①sinB的值是 ;
②畫出△ABC關于直線l對稱的△A1B1C1(A與A1,B與B1,C與C1相對應).連接AA1,BB1,并計算梯形AA1B1B的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
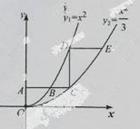
如圖,平行于x軸的直線AC分別交函數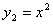 (x≥o)與
(x≥o)與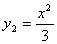 (x≥0)的圖象于B、C兩 點,過點c作y軸的平行線交y1的圖象于點D,直線DE∥AC,交y2的圖象于點E,則
(x≥0)的圖象于B、C兩 點,過點c作y軸的平行線交y1的圖象于點D,直線DE∥AC,交y2的圖象于點E,則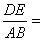
查看答案和解析>>
科目:初中數學 來源: 題型:
(1)食品安全是關乎民生的問題,在食品中添加過量的添加劑對人體有害,但適量的添加劑對人體無害且有利于食品的儲存和運輸.某飲料加工廠生產的A、B兩種飲料均需加入同種添加劑,A飲料每瓶需加該添加劑2克,B飲料每瓶需加該添加劑3克,已知270克該添加劑恰好生產了A、B兩種飲料共1OO瓶,問A、B兩種飲料各生產了多少瓶?
查看答案和解析>>
科目:初中數學 來源: 題型:
復習課中,教師給出關于x的函數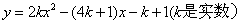 .
.
教師:請獨立思考,并把探索發現的與該函數有關的結論(性質)寫道黑板上.
學生思考后,黑板上出現了一些結論,教師作為活動醫院,又補充一些結論,并從中選擇如下四條:
①存在函數,其圖像經過(1,0)點;
②函數圖像與坐標軸總有三個不同的交點;
③當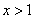 時,
時, 不是y隨x的增大而增大就是y隨x的增大而減小;
不是y隨x的增大而增大就是y隨x的增大而減小;
④若函數有最大值,則最大值必為正數,若函數有最小值,則最小值必為負數。
教師:請你分別判斷四條結論的真假,并給出理由.最后簡單寫出解決問題時所用的數學方法。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com