
如圖,在△ABC上,點D、E分別是AC、BC邊上的點,AE與BD交于點O,且CD=CE,∠1=∠2.
(1)求證:四邊形ABDE是等腰梯形;
(2)若EC=2,BE=1,∠AOD=2∠1,求AB的長.


【考點】等腰梯形的判定.
【分析】(1)由等腰三角形的性質得出∠CDE=∠CED,由三角形的外角性質和已知條件得出∠AED=∠BDE,證出OD=OE,由AAS證明△AOD≌△BOE,得出AD=BE,OA=OB,由等腰三角形的性質得出∠OAB=∠OBA,再由對頂角相等和三角形內角和定理得出∠OAB=∠OBA=∠ODE=∠OED,證出DE∥AB,即可得出結論;
(2)由三角形的外角性質和已知條件得出∠1=∠OED,證出AD=ED=BE=1,由平行線的性質得出△CDE∽△CAB,得出對應邊成比例,即可得出AB的長.
【解答】(1)證明:∵CD=CE,
∴∠CDE=∠CED,
∵∠CDE=∠2+∠AED,∠CED=∠1+∠BDE,∠1=∠2,
∴∠AED=∠BDE,
∴OD=OE,
在△AOD和△BOE中,
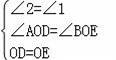
 ,
,
∴△AOD≌△BOE(AAS),
∴AD=BE,OA=OB,
∴∠OAB=∠OBA,
∵∠AOD=∠BOE,
∴∠OAB=∠OBA=∠ODE=∠OED,
∴DE∥AB,
∴四邊形ABDE是等腰梯形;
(2)解:∵∠AOD=2∠1=∠ODE+∠OED,∠OED=∠ODE,
∴∠1=∠OED,
∴AD=ED=BE=1,
∵DE∥AB,
∴△CDE∽△CAB,
∴
 ,
,
即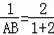
 ,
,
解得:AB=
 .
.
【點評】本題考查了等腰梯形的判定、等腰三角形的判定與性質、全等三角形的判定與性質、相似三角形的判定與性質等知識;熟練掌握等腰梯形的判定,證明三角形全等和三角形相似是解決問題的關鍵.


科目:初中數學 來源: 題型:
甲、乙兩名同學某學期的四次數學測試成績(單位:分)如下表:
| 第一次 | 第二次 | 第三次 | 第四次 | |
| 甲 | 87 | 95 | 85 | 93 |
| 乙 | 80 | 80 | 90 | 90 |
據上表計算,甲、乙兩名同學四次數學測試成績的方差分別為S甲2=17、S乙2=25,下列說法正確的是( )
A.甲同學四次數學測試成績的平均數是89分
B.甲同學四次數學測試成績的中位數是90分
C.乙同學四次數學測試成績的眾數是80分
D.乙同學四次數學測試成績較穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
某商店銷售一種襯衫,四月份的營業額為5000元;為了擴大銷售,在五月份將每件襯衫按原價的8折銷售,結果銷售量比四月份增加了40件,營業額比四月份增加了600元。求四月份每件襯衫的售價。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com