
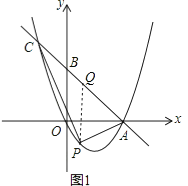
【題目】如圖1,已知直線l:y=﹣x+2與x軸交于點A、與y軸交于點B.拋物線y=ax2+bx+c(a≠0)經過O、A兩點,與直線l交于點C,點C的橫坐標為﹣1.
(1)求該拋物線的函數表達式;
(2)若點P是位于直線l下方拋物線上的一個動點,且不與點A、點C重合,連接PA、PC.設△PAC的面積為S,求當S取得最大值時點P的坐標,并求S的最大值;
(3)如圖2,設拋物線的頂點為D,連接AD、BD.點E是對稱軸m上一點,F是拋物線上一點,請直接寫出當△DEF與△ABD相似時點E的坐標.
【答案】
(1)
解:當x=﹣1時,y=﹣x+2=3,則C(﹣1,3),
當y=0時,﹣x+2=0,解得x=2,則A(2,0),
∵拋物線過點O(0,0)、A(2,0),
設拋物線解析式為y=ax( x﹣2 ),
將點C(﹣1,3)代入得3=﹣a(﹣1﹣2 ),解得a=1,
∴該拋物線解析式為y=x( x﹣2 ),即y=x2﹣2x
(2)
解:設P(m,m2﹣2m),過點P作PQ∥y軸,交直線l于點Q,如圖1,則Q(m,﹣m+2),
∴PQ=(﹣m+2 )﹣(m2﹣2m)=﹣m2+m+2,
∴S=S△PQC+S△PQA= ![]() (2+1)PQ=﹣
(2+1)PQ=﹣ ![]() m2+
m2+ ![]() m+3=﹣
m+3=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴當m= ![]() 時,S有最大值,最大值為
時,S有最大值,最大值為 ![]() ,
,
把m= ![]() 代入m2﹣2m得m2﹣2m=﹣
代入m2﹣2m得m2﹣2m=﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:設F點坐標為(t,t2﹣2t),
當x=1時,y=x2﹣2x=﹣1,則D(1,﹣1),當x=0時,y=﹣x+2=2,則B(0,2),
∵AB2=22+22=8,AD2=12+12=2,DB2=12+(2+1)2=10,
∴AB2+AD2=DB2,
∴△ABD為直角三角形,∠BAD=90°,
如圖2,
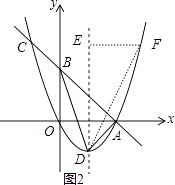
當△DEF∽△BAD,則∠DEF=∠BAD=90°, ![]() =
= ![]() ,即DE:2
,即DE:2 ![]() =EF:
=EF: ![]() ,
,
∴DE=2EF,
∵EF⊥DE,
∴E(1,t2﹣2t),
∴t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,此時E點坐標為(1,3);
當△DEF∽△DAB,則∠DEF=∠BAD=90°, ![]() =
= ![]() ,即DE:
,即DE: ![]() =EF:2
=EF:2 ![]() ,
,
∴DE= ![]() EF,
EF,
∵EF⊥DE,
∴E(1,t2﹣2t),
∴t2﹣2t+1= ![]() (t﹣1),解得t1=1(舍去),t2=
(t﹣1),解得t1=1(舍去),t2= ![]() ,此時E點坐標為(1,﹣
,此時E點坐標為(1,﹣ ![]() );
);
如圖3,
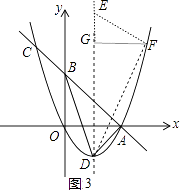
當△DFE∽△BAD,則∠DFE=∠BAD=90°,∠FDE=∠ADB,
過F點作FG⊥DE于G,則△DGF∽△BAD,同樣方法可得G(1,3),則F(3,3),
∵GF2=GEGD,即22=GE4,
∴GE=1,
∴此時E點坐標為(1,4);
當△DFE∽△DAB,則∠DFE=∠BAD=90°,用同樣方法可得E點坐標為(1, ![]() ),
),
綜上所述,E點坐標為(1,3),(1,4),(1, ![]() ),(1,﹣
),(1,﹣ ![]() ).
).
【解析】(1)先根據一次函數圖象上點的坐標特征求出C(﹣1,3),A(2,0),再設交點式y=ax( x﹣2 ),然后把點C點坐標代入求出a即可得到該拋物線解析式為y=x2﹣2x;(2)設P(m,m2﹣2m),過點P作PQ∥y軸,交直線l于點Q,如圖1,則Q(m,﹣m+2),則PQ=﹣m2+m+2,根據三角形面積公式,利用S=S△PQC+S△PQA可得到S=﹣ ![]() m2+
m2+ ![]() m+3,然后根據二次函數的性質解決最值問題(3)設F點坐標為(t,t2﹣2t),先確定D(1,﹣1),B(0,2),再利用勾股定理的逆定理證明△ABD為直角三角形,∠BAD=90°,然后分類討論:如圖2,當△DEF∽△BAD,則∠DEF=∠BAD=90°,利用相似比得DE=2EF,由于EF⊥DE,則E(1,t2﹣2t),所以t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,易得此時E點坐標為(1,3);當△DEF∽△DAB,則∠DEF=∠BAD=90°,
m+3,然后根據二次函數的性質解決最值問題(3)設F點坐標為(t,t2﹣2t),先確定D(1,﹣1),B(0,2),再利用勾股定理的逆定理證明△ABD為直角三角形,∠BAD=90°,然后分類討論:如圖2,當△DEF∽△BAD,則∠DEF=∠BAD=90°,利用相似比得DE=2EF,由于EF⊥DE,則E(1,t2﹣2t),所以t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,易得此時E點坐標為(1,3);當△DEF∽△DAB,則∠DEF=∠BAD=90°, ![]() =
= ![]() ,利用相似比得DE=
,利用相似比得DE= ![]() EF,
EF,
由EF⊥DE得到E(1,t2﹣2t),則t2﹣2t+1= ![]() (t﹣1),解得t1=1(舍去),t2=
(t﹣1),解得t1=1(舍去),t2= ![]() ,易得此時E點坐標為(1,﹣
,易得此時E點坐標為(1,﹣ ![]() );如圖3,當△DFE∽△BAD,則∠DFE=∠BAD=90°,∠FDE=∠ADB,過F點作FG⊥DE于G,則△DGF∽△BAD,用前面方法可得G(1,3),則F(3,3),利用GF2=GEGD可計算出GE=1,則此時E點坐標為(1,4);當△DFE∽△DAB,則∠DFE=∠BAD=90°,用同樣方法可得E點坐標為(1,
);如圖3,當△DFE∽△BAD,則∠DFE=∠BAD=90°,∠FDE=∠ADB,過F點作FG⊥DE于G,則△DGF∽△BAD,用前面方法可得G(1,3),則F(3,3),利用GF2=GEGD可計算出GE=1,則此時E點坐標為(1,4);當△DFE∽△DAB,則∠DFE=∠BAD=90°,用同樣方法可得E點坐標為(1, ![]() ).
).
【考點精析】根據題目的已知條件,利用一次函數的性質和二次函數的圖象的相關知識可以得到問題的答案,需要掌握一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小;二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的方程(1﹣2k)x2﹣2![]() x﹣1=0
x﹣1=0
(1)若此方程為一元一次方程,求k的值.
(2)若此方程為一元二次方程,且有實數根,試求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在同一平面內,△ABC和△ABD如圖①放置,其中AB=BD.
小明做了如下操作:
將△ABC繞著邊AC的中點旋轉180°得到△CEA,將△ABD繞著邊AD的中點旋轉180°得到△DFA,如圖②,請完成下列問題:
(1)試猜想四邊形ABDF是什么特殊四邊形,并說明理由;
(2)連接EF,CD,如圖③,求證:四邊形CDEF是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數圖象經過點(-1,2).
(1)求此正比例函數的表達式;
(2)畫出這個函數圖象;
(3)點(2,-5)是否在此函數圖象上?
(4)若這個圖象還經過點A(a,8),求點A的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是兩個可以自由轉動的轉盤,轉盤A被分成三個面積相等的扇形,轉盤B被分成兩個面積相等的扇形. 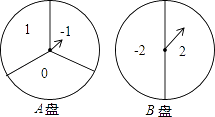
(1)轉動轉盤A一次,所得到的數字是負數的概率為
(2)轉動兩個轉盤各一次,請用列表法或畫樹狀圖法求所得到的數字均是負數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列結論:
①abc<0;②b2﹣4ac>0;③3a+c<0;④16a+4b+c>0.
其中正確結論的個數是( )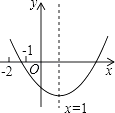
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有四張背面相同的紙牌A,B,C,D,其正面分別畫有四個不同的幾何圖形,將這四張紙牌背面朝上洗勻后放在桌面上. 
(1)小紅從中隨機摸出一張,求摸出的牌面圖形是中心對稱圖形的概率;
(2)小明從這四張紙牌中隨機摸出兩張,用樹狀圖或表格法,求摸出的兩張牌面圖形都是中心對稱圖形的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,Rt△ABC中,∠ABC=90°,BC<AB<2BC.在AB邊上取一點M,使AM=BC,過點A作AE⊥AB且AE=BM,連接EC,再過點A作AN∥EC,交直線CM、CB于點F、N.
(1)證明:∠AFM=45°;
(2)若將題中的條件“BC<AB<2BC”改為“AB>2BC”,其他條件不變,請你在圖2的位置上畫出圖形,(1)中的結論是否仍然成立?如果成立,請說明理由;如果不成立,請猜想∠AFM的度數,并說明理由.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了應對金融危機,節儉開支,我區某康莊工程指揮部,要對某路段建設工程進行招標,從甲、乙兩個工程隊的投標書中得知:每天需支付甲隊的工程款1.5萬元,乙隊的工程款1.1萬元.甲、乙兩個工程隊實際施工方案如下:
(1)甲隊單獨完成這項工程剛好能夠如期完成;
(2)乙隊單獨完成這項工程要比規定的時間多用10天;
(3)若甲、乙兩隊合作8天,余下的由乙隊單獨做也正好如期完成.
試問:在不耽誤工期的前提下,你覺得哪一種施工方案最節省工程款?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com