亮點激活精編提優100分大試卷系列答案
智趣寒假作業云南科技出版社系列答案科目：初中數學 來源： 題型：
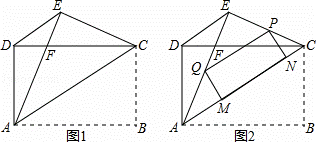
如圖1，矩形ABCD中，AB=4，AD=3，把矩形沿直線AC折疊，使點B落在點E處，AE交CD于點F，連接DE．
（1）求證：△DEC≌△EDA；
（2）求DF的值；
（3）如圖2，若P為線段EC上一動點，過點P作△AEC的內接矩形，使其定點Q落在線段AE上，定點M、N落在線段AC上，當線段PE的長為何值時，矩形PQMN的面積最大？并求出其最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
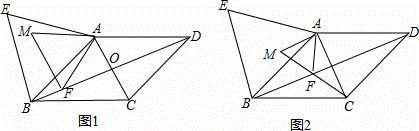
如圖1，在菱形ABCD中，對角線AC與BD相交于點O，AB=13，BD=24，在菱形ABCD的外部以AB為邊作等邊三角形 ABE．點F是對角線BD上一動點（點F不與點B重合），將線段AF繞點A順時針方向旋轉60°得到線段AM，連接FM．
（1）求AO的長；
（2）如圖2，當點F在線段BO上，且點M，F，C三點在同一條直線上時，求證：AC=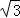
AM；
（3）連接EM，若△AEM的面積為40，請直接寫出△AFM的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖分別是某班全體學生上學時乘車、步行、騎車人數的分布直方圖和扇形統計圖（兩圖都不完整），下列結論錯誤的是（ ）
|
| A． | 該班總人數為50人 | B． | 步行人數為30人 |
|
| C． | 乘車人數是騎車人數的2.5倍 | D． | 騎車人數占20% |
查看答案和解析>>
科目：初中數學 來源： 題型：
某企業設計了一款工藝品，每件的成本是50元，為了合理定價，投放市場進行試銷．據市場調查，銷售單價是100元時，每天的銷售量是50件，而銷售單價每降低1元，每天就可多售出5件，但要求銷售單價不得低于成本．
（1）求出每天的銷售利潤y（元）與銷售單價x（元）之間的函數關系式；
（2）求出銷售單價為多少元時，每天的銷售利潤最大？最大利潤是多少？
（3）如果該企業要使每天的銷售利潤不低于4000元，且每天的總成本不超過7000元，那么銷售單價應控制在什么范圍內？（每天的總成本=每件的成本×每天的銷售量）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
= 
．
，求代數式（x+1）2﹣2x+y（y﹣2x）的值．