
【題目】在菱形![]() 中,
中,![]() 為直線
為直線![]() 上的點,
上的點,![]() 為直線
為直線![]() 上的點,分別連接
上的點,分別連接![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,點
,點![]() 在線段
在線段![]() 上,點
上,點![]() 在線段
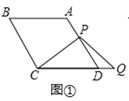
在線段![]() 的延長線上,如圖①,易證:
的延長線上,如圖①,易證:![]() (不需證明);
(不需證明);
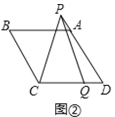
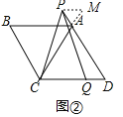
(2)如圖②,若∠B=120°,點![]() 在線段
在線段![]() 上,點
上,點![]() 在線段
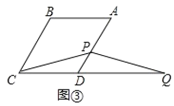
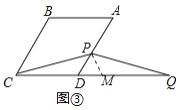
在線段![]() 的延長線上,如圖③,猜想線段
的延長線上,如圖③,猜想線段![]() ,
,![]() 和
和![]() 之間有怎樣的數量關系?請直接寫出對圖②,圖③的猜想,并選擇其中一種情況給予證明.
之間有怎樣的數量關系?請直接寫出對圖②,圖③的猜想,并選擇其中一種情況給予證明.
【答案】(1)見解析;(2)②結論:![]() ;③結論:
;③結論:![]() ,證明見解析
,證明見解析
【解析】
(1)連接AC,過P作PE∥CD交AC于E,由四邊形ABCD是菱形,∠B=60°,得出△ACD是等邊三角形,∠PDQ=120°,由PE∥CD,得出△APE是等邊三角形,∠PEC=120°,由AAS證得△PCE≌△PQD,得出PE=DQ,AP=DQ,即可得出結論;
(2)①結論:![]() .如圖②中,延長
.如圖②中,延長![]() 到
到![]() ,使得
,使得![]() ,連接
,連接![]() .只要證明
.只要證明![]() 是等邊三角形,
是等邊三角形,![]() 即可解決問題;
即可解決問題;
②結論:![]() .如圖③中,在
.如圖③中,在![]() 上截取
上截取![]() ,連接
,連接![]() .只要證明
.只要證明![]() 是等邊三角形,
是等邊三角形,![]() 即可解決問題;
即可解決問題;
解:(1)證明:連接AC,過P作PE∥CD交AC于E,如圖①所示:
∵四邊形ABCD是菱形,
∴AD=CD=AB,∠ADC=∠B=60°,
∴△ACD是等邊三角形,∠PDQ=120°,
∴AC=AD,∠DAC=∠ACD=60°,
∵PE∥CD,
∴∠AEP=∠ACD=60°,∠APE=∠ADC=60°,
∴△APE是等邊三角形,∠PEC=120°,
∴AE=PE=AP,
∵PC=PQ,
∴∠PCQ=∠Q,
∵∠ACD=∠ECP+∠PCQ,∠ADC=∠DPQ+∠Q,
∴∠ECP=∠DPQ,
在△PCE和△PQD中,
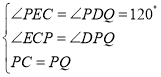 ,
,
∴△PCE≌△PQD(AAS),
∴PE=DQ,
∴AP=DQ,
∴DQ+PD=AP+PD=AD=AB;

(2)②結論:![]() .
.
理由:如圖②中,延長![]() 到
到![]() ,使得
,使得![]() ,連接
,連接![]() .
.
![]() 四邊形
四邊形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,![]() 都是等邊三角形,
都是等邊三角形,
![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
③結論:![]() .
.
理由:如圖③中,在![]() 上截取
上截取![]() ,連接
,連接![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網格中,點![]() ,
,![]() ,
,![]() ,
,![]() 均在格點上,點
均在格點上,點![]() 是在直線
是在直線![]() 上的動點,連
上的動點,連![]() ,點
,點![]() 是點
是點![]() 關于直線
關于直線![]() 的對稱點.
的對稱點.
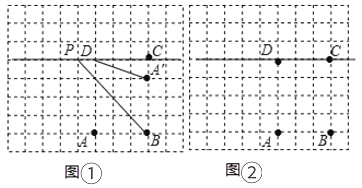
(1)在圖①中,當![]() (點
(點![]() 在點
在點![]() 的左側)時,計算
的左側)時,計算![]() 的值等于______.
的值等于______.
(2)當![]() 取得最小值時,請在如圖②所示的網格中,用無刻度的直尺畫出點
取得最小值時,請在如圖②所示的網格中,用無刻度的直尺畫出點![]() ,并簡要說明點
,并簡要說明點![]() 的位置是如何找到的.(不要求證明)
的位置是如何找到的.(不要求證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將矩形紙片OABC放在平面直角坐標系中,0為坐標原點,點A在y軸上,點C在x軸上,點B的坐標是(8,6),點P是邊AB上的一個動點,將△OAP沿OP折疊,使點A落在點Q處.
(1)如圖①,當點Q恰好落在OB上時.求點p的坐標;
(2)如圖②,當點P是AB中點時,直線OQ交BC于M點.
①求證:MB=MQ;②求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉辦朗誦比賽,比賽結束后,對學生的成績進行了統計.繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
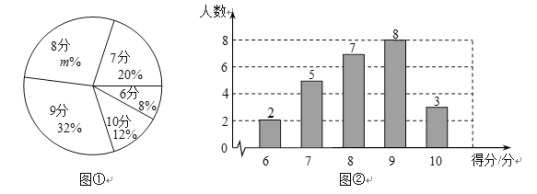
(1)參加這次比賽的人數為 ,圖①中![]() 的值為 ;
的值為 ;
(2)求統計的這組學生朗誦比賽成績數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是邊AC上的動點,BD的垂直平分線交BC于點E,連接DE,若△CDE為直角三角形,則BE的長為_____.
+2,D是邊AC上的動點,BD的垂直平分線交BC于點E,連接DE,若△CDE為直角三角形,則BE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市在創建全國文明城市過程中,決定購買A,B兩種樹苗對某路段道路進行綠化改造,已知購買A種樹苗8棵,B種樹苗3棵,需要950元;若購買A種樹苗5棵,B種樹苗6棵,則需要800元.
(1)求購買A,B兩種樹苗每棵各需多少元?
(2)考慮到綠化效果和資金周轉,購進A種樹苗不能少于48棵,且用于購買這兩種樹的資金不能超過7500元,若購進這兩種樹苗共100棵,則有哪幾種購買方案?
(3)某包工隊承包種植任務,若種好一棵A種樹苗可獲工錢30元,種好一棵B種樹苗可獲工錢20元,在第(2)問的各種購買方案中,種好這100棵樹苗,哪一種購買方案所付的種植工錢最少?最少工錢是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣政府計劃撥款34000元為福利院購買彩電和冰箱,已知商場彩電標價為2000元/臺,冰箱標價為1800元/臺,如按標價購買兩種家電,恰好將撥款全部用完.
(1)問原計劃購買的彩電和冰箱各多少臺?
(2)購買的時候恰逢商場正在進行促銷活動,全場家電均降價![]() 進行銷售,若在不增加縣政府實際負擔的情況下,能否比原計劃多購買3臺冰箱?請通過計算回答.
進行銷售,若在不增加縣政府實際負擔的情況下,能否比原計劃多購買3臺冰箱?請通過計算回答.
查看答案和解析>>
科目:初中數學 來源: 題型:
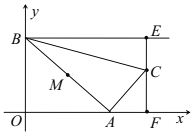
【題目】如圖,點![]() 是
是![]() 軸非負半軸上的動點,點
軸非負半軸上的動點,點![]() 坐標為
坐標為![]() ,
,![]() 是線段
是線段![]() 的中點,將點
的中點,將點![]() 繞點
繞點![]() 順時針方向旋轉90°得到點
順時針方向旋轉90°得到點![]() ,過點
,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,過點
,過點![]() 作
作![]() 軸的垂線與直線
軸的垂線與直線![]() 相交于點
相交于點![]() ,連接
,連接![]() ,
,![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(2)設![]() 的面積為
的面積為![]() ,當點
,當點![]() 在線段
在線段![]() 上時,求
上時,求![]() 與
與![]() 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)當![]() 為何值時,
為何值時,![]() 取得最小值.
取得最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
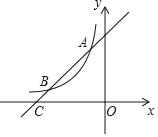
【題目】如圖,一次函數y=x+4的圖象與反比例函數y=![]() (k為常數且k≠0)的圖象交于A(﹣1,a),B兩點,與x軸交于點C.
(k為常數且k≠0)的圖象交于A(﹣1,a),B兩點,與x軸交于點C.
(1)求a,k的值及點B的坐標;
(2)若點P在x軸上,且S△ACP=![]() S△BOC,直接寫出點P的坐標.
S△BOC,直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com