
【題目】如圖,![]() 中,以
中,以![]() 為直徑作⊙
為直徑作⊙![]() ,交
,交![]() 于點
于點![]() ,
,![]() 為弧
為弧![]() 上一點,連接
上一點,連接![]() 、
、![]() 、
、![]() ,交
,交![]() 于點
于點![]() .
.
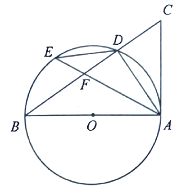
(1)若![]() ,求證:
,求證:![]() 為⊙
為⊙![]() 的切線;
的切線;
(2)若![]() ,求證:
,求證:![]() 平分
平分![]() ;
;
(3)在(2)的條件下,若![]() ,求⊙
,求⊙![]() 的半徑.
的半徑.
【答案】(1)詳見解析;(2)詳見解析;(3)![]() .
.
【解析】
(1)根據AB為⊙![]() 直徑,得出
直徑,得出![]() =90°,即
=90°,即![]() °,
°,![]() ,
,![]() ,推出
,推出![]() ,即
,即![]() °,
°,
所以![]() =
=![]() =90°,得出AC為⊙
=90°,得出AC為⊙![]() 的切線;(2)證明
的切線;(2)證明![]() , 得到
, 得到![]() ,因為
,因為![]() ,所以
,所以![]() ,即可得到AE平分
,即可得到AE平分![]() ;(3)過點F作FH⊥AB于H可證
;(3)過點F作FH⊥AB于H可證![]() ,可得AH=AD=4,FH=DF=2;可證
,可得AH=AD=4,FH=DF=2;可證![]() 故
故![]() ;BH=x,則BD=2x,BF=2x-2,利用勾股定理可得
;BH=x,則BD=2x,BF=2x-2,利用勾股定理可得![]() ,
,![]() ;解得BH=
;解得BH=![]() ,AB=BH+AH=
,AB=BH+AH=![]() ,由AO=
,由AO=![]() AB=
AB=![]() ,即可得⊙
,即可得⊙![]() 的半徑.
的半徑.
(1)證明:∵AB為⊙![]() 直徑,
直徑,
∴![]() =90°,
=90°,
∴![]() °,
°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() °,
°,
即![]() °,
°,
∴AC為⊙![]() 的切線;
的切線;
(2)證明:∵![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
即AE平分![]() .
.
(3)解:過點F作FH⊥AB于H.
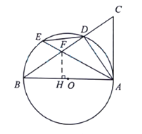
∴![]() °;
°;
又∵![]() ,AF=AF,
,AF=AF,
∴![]() ;
;
∴AH=AD=4,FH=DF=2;
∵![]() °,
°,![]() ,
,
∴![]() ,
,
∴![]() ;
;
設BH=x,則BD=2x,BF=2x-2,
∴![]() ,
,
∴![]() ;
;
∴x=0(舍)或x=![]() ;
;
∴BH=![]() ,AB=BH+AH=
,AB=BH+AH=![]() ;
;
∴AO=![]() AB=
AB=![]() ;
;
∴⊙![]() 的半徑為
的半徑為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,直線y1=﹣x+4,y2=![]() x+b都與雙曲線y=
x+b都與雙曲線y=![]() 交于點A(1,m),這兩條直線分別與x軸交于B,C兩點.
交于點A(1,m),這兩條直線分別與x軸交于B,C兩點.
(1)求y與x之間的函數關系式;
(2)直接寫出當x>0時,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若點P在x軸上,連接AP把△ABC的面積分成1:3兩部分,求此時點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點![]() 在正方形
在正方形![]() 的對角線
的對角線![]() 上,正方形
上,正方形![]() 的邊長是
的邊長是![]() ,
,![]() 的兩條直角邊
的兩條直角邊![]() 分別交邊
分別交邊![]() 于點
于點![]() .
.
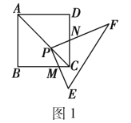
(1)操作發現:如圖2,固定點![]() ,使
,使![]() 繞點
繞點![]() 旋轉,當
旋轉,當![]() 時,四邊形
時,四邊形![]() 是正方形.
是正方形.
填空:①當![]() 時,四邊形
時,四邊形![]() 的邊長是_____;
的邊長是_____;
②當![]() (
(![]() 是正實數)時,四邊形
是正實數)時,四邊形![]() 的面積是______;
的面積是______;
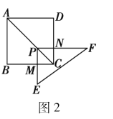
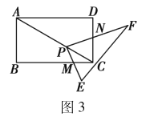
(2)猜想論證:如圖3,將四邊形![]() 的形狀改變為矩形,
的形狀改變為矩形,![]() ,
,![]() ,點
,點![]() 在矩形
在矩形![]() 的對角線
的對角線![]() ,
,![]() 的兩條直角邊
的兩條直角邊![]() 分別交邊
分別交邊![]() 于點
于點![]() ,固定點
,固定點![]() ,使
,使![]() 繞點
繞點![]() 旋轉,則
旋轉,則![]() ______;
______;
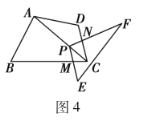
(3)拓展探究:如圖4,當四邊形![]() 滿足條件:
滿足條件:![]() ,
,![]() ,時,點
,時,點![]() 在對角線
在對角線![]() 上,
上,![]() 分別交邊
分別交邊![]() 于點
于點![]() ,固定點
,固定點![]() ,使
,使![]() 繞點
繞點![]() 旋轉,請探究
旋轉,請探究![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】外線投籃是籃球隊常規訓練的重要項目之一,下列圖表中數據是甲、乙、丙三人每人十次投籃測試的成績.測試規則為連續投籃十個球為一次,投進籃筐一個球記為1分.
運動員甲測試成績表
測試序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成績(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
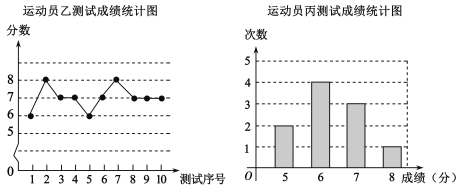
(1)寫出運動員乙測試成績的眾數和中位數;
(2)在他們三人中選擇一位投籃成績優秀且較為穩定的選手作為中鋒,你認為選誰更合適?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
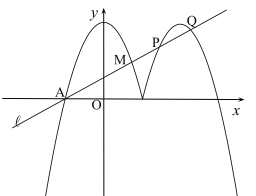
【題目】在平面直角坐標系中,拋物線![]() 的最高點的縱坐標是2.
的最高點的縱坐標是2.
(1)求拋物線的表達式;
(2)將拋物線在![]() 之間的部分記為圖象
之間的部分記為圖象![]() ,將圖象
,將圖象![]() 沿直線x=1翻折,翻折后圖象記為
沿直線x=1翻折,翻折后圖象記為![]() ,圖象
,圖象![]() 和
和![]() 組成G,直線
組成G,直線![]() :
:![]()
![]() 和圖象G在x軸上方的部分有兩個公共點,求k的取值范圍;
和圖象G在x軸上方的部分有兩個公共點,求k的取值范圍;
(3)直線![]() :
:![]() 與圖象G在x軸上方的部分分別交于A、M、P、Q四點,若AM=2PQ,求
與圖象G在x軸上方的部分分別交于A、M、P、Q四點,若AM=2PQ,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,把
,把![]() 的各邊進行下列變換:①各邊的長度分別擴大為原來的3倍;②各邊的長度分別縮小為原來的
的各邊進行下列變換:①各邊的長度分別擴大為原來的3倍;②各邊的長度分別縮小為原來的![]() ;③各邊的長度分別增加2;④各邊的長度分別平方.其中得到的三角形與
;③各邊的長度分別增加2;④各邊的長度分別平方.其中得到的三角形與![]() 相似的有( )
相似的有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,點G在直徑DF的延長線上,∠D=∠G=30°.
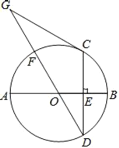
(1)判斷CG與圓O的關系,并說明理由;
(2)若CD=6,求線段GF的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】超速行駛被稱為“馬路第一殺手”為了讓駕駛員自覺遵守交通規則,湖潯大道公路檢測中心在一事故多發地段安裝了一個測速儀器,如圖所示,已知檢測點設在距離公路10米的A處,測得一輛汽車從B處行駛到C處所用時間為1.35秒.已知∠B=45°,∠C=30°.
(1)求B,C之間的距離(結果保留根號);
(2)如果此地限速為70km/h,那么這輛汽車是否超速?請說明理由.(參考數據;![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋子中裝有紅、白兩種顏色的小球,這些球除顏色外完全相同,其中紅球1個,若從中隨機摸出一個球,這個球是白球的概率為![]()
(1)求袋子中白球的個數
(2)隨機摸出一個球后,放回并攪勻,再隨機摸出一個球,請用畫樹狀圖或列表的方法,求兩次都摸到白球的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com