下面的數列是一個等差數列,
8,15,22,29,36,…
它們前n-1個數乘積的末尾0的個數比前n個數相乘的積的末尾0的個數少3個.求n的最小值.
【答案】
分析:本題根據前n-1個數乘積的末尾0的個數比前n個數相乘的積的末尾0的個數少3個,可得第n個數是125的倍數,根據數列通項a
n=7n+1,可得7n+1=125k,變形為n=
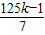
=18k-
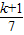
,得到最小k的值,從而求解.
解答:解:如果要滿足題目條件,則10是要求因子中有2和5,一對在數末尾出一個0,
觀察數列,將以上數乘在一起,因子5的數量要少于2的數量.
所以要第n個數是125的倍數.
易知數列通項a
n=7n+1,
所以a
(n-1)=7n-6,
設7n+1=125k,n=
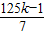
=18k-
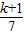
,
得最小k=6,此時n=107.
答:n的最小值是107.
點評:此題考查了數的整除性,本題關鍵是熟悉等差數列的通項公式及第n個數是125的倍數.

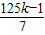 =18k-
=18k-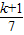 ,得到最小k的值,從而求解.
,得到最小k的值,從而求解.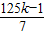 =18k-
=18k-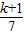 ,
,
