
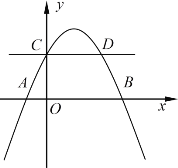
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]()
![]() ,
,![]() 兩點(diǎn),交
兩點(diǎn),交![]() 軸于點(diǎn)C,與過(guò)點(diǎn)C且平行于x軸的直線交于另一點(diǎn)
軸于點(diǎn)C,與過(guò)點(diǎn)C且平行于x軸的直線交于另一點(diǎn)![]() ,點(diǎn)P是拋物線上一動(dòng)點(diǎn).
,點(diǎn)P是拋物線上一動(dòng)點(diǎn).
(1)求拋物線解析式及點(diǎn)D的坐標(biāo);
(2)點(diǎn)![]() 在
在![]() 軸上,若以
軸上,若以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點(diǎn)的四邊形是平行四邊形,求此時(shí)點(diǎn)
為頂點(diǎn)的四邊形是平行四邊形,求此時(shí)點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)過(guò)點(diǎn)![]() 作直線CD的垂線,垂足為
作直線CD的垂線,垂足為![]() ,若將
,若將![]() 沿
沿![]() 翻折,點(diǎn)
翻折,點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)為
的對(duì)應(yīng)點(diǎn)為![]() .是否存在點(diǎn)
.是否存在點(diǎn)![]() ,使
,使![]() 恰好落在
恰好落在![]() 軸上?若存在,求出此時(shí)點(diǎn)P的坐標(biāo);若不存在,說(shuō)明理由.
軸上?若存在,求出此時(shí)點(diǎn)P的坐標(biāo);若不存在,說(shuō)明理由.
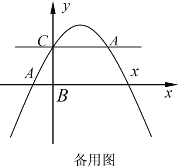
【答案】(1)![]() ;點(diǎn)
;點(diǎn)![]() 坐標(biāo)為
坐標(biāo)為![]() ; (2)P1(0,2); P2(
; (2)P1(0,2); P2(![]() ,-2);P3(
,-2);P3(![]() ,-2) ; (3)滿足條件的點(diǎn)
,-2) ; (3)滿足條件的點(diǎn)![]() 有兩個(gè),其坐標(biāo)分別為:(
有兩個(gè),其坐標(biāo)分別為:(![]() ,
, ![]() ),(
),(![]() ,
,![]() ).
).
【解析】
1)用待定系數(shù)法可得出拋物線的解析式,令y=2可得出點(diǎn)D的坐標(biāo)
(2)分兩種情況進(jìn)行討論,①當(dāng)AE為一邊時(shí),AE∥PD,②當(dāng)AE為對(duì)角線時(shí),根據(jù)平行四邊形對(duì)頂點(diǎn)到另一條對(duì)角線距離相等,求解點(diǎn)P坐標(biāo)
(3)結(jié)合圖形可判斷出點(diǎn)P在直線CD下方,設(shè)點(diǎn)P的坐標(biāo)為(![]() ,
,![]() ),分情況討論,①當(dāng)P點(diǎn)在y軸右側(cè)時(shí),②當(dāng)P點(diǎn)在y軸左側(cè)時(shí),運(yùn)用解直角三角形及相似三角形的性質(zhì)進(jìn)行求解即可
),分情況討論,①當(dāng)P點(diǎn)在y軸右側(cè)時(shí),②當(dāng)P點(diǎn)在y軸左側(cè)時(shí),運(yùn)用解直角三角形及相似三角形的性質(zhì)進(jìn)行求解即可
(1)∵拋物線![]() 經(jīng)過(guò)
經(jīng)過(guò)![]()
![]() ,
,![]()
![]() 兩點(diǎn),
兩點(diǎn),
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴拋物線解析式為:![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,解得:
,解得:![]() ,
,![]() (舍),即:點(diǎn)
(舍),即:點(diǎn)![]() 坐標(biāo)為
坐標(biāo)為![]() .
.
(2)∵![]() ,
,![]() 兩點(diǎn)都在
兩點(diǎn)都在![]() 軸上,∴
軸上,∴![]() 有兩種可能:
有兩種可能:
①當(dāng)![]() 為一邊時(shí),
為一邊時(shí),![]() ∥
∥![]() ,此時(shí)點(diǎn)
,此時(shí)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合(如圖1),∴
重合(如圖1),∴![]() ,
,
②當(dāng)![]() 為對(duì)角線時(shí),
為對(duì)角線時(shí),![]() 點(diǎn)、
點(diǎn)、![]() 點(diǎn)到直線
點(diǎn)到直線![]() (即
(即![]() 軸)的距離相等,
軸)的距離相等,
∴![]() 點(diǎn)的縱坐標(biāo)為
點(diǎn)的縱坐標(biāo)為![]() (如圖2),
(如圖2),
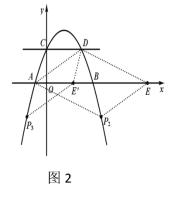
把![]() 代入拋物線的解析式,得:
代入拋物線的解析式,得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() ,
,![]() ,
,
綜上所述:![]() ;
; ![]()
![]() ;
;![]()
![]() .
.
(3)存在滿足條件的點(diǎn)![]() ,顯然點(diǎn)
,顯然點(diǎn)![]() 在直線
在直線![]() 下方,設(shè)直線
下方,設(shè)直線![]() 交
交![]() 軸于
軸于![]() ,
,
點(diǎn)![]() 的坐標(biāo)為(
的坐標(biāo)為(![]() ,
,![]() ),
),
①當(dāng)![]() 點(diǎn)在
點(diǎn)在![]() 軸右側(cè)時(shí)(如圖3),
軸右側(cè)時(shí)(如圖3),
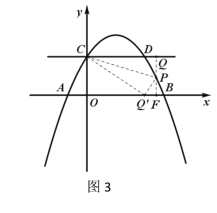
![]() ,
,
![]()
![]()
![]() ,
,
又∵![]()
![]() ,
,
![]() ∴
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]()
![]() ,∴
,∴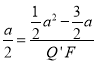 ,∴
,∴![]() ,
,
∴![]()
![]() ,
,![]() =
=![]() =
=![]() ,
,
即![]() ,∴點(diǎn)
,∴點(diǎn)![]() 的坐標(biāo)為(
的坐標(biāo)為(![]() ,
,![]() ),
),
②當(dāng)![]() 點(diǎn)在
點(diǎn)在![]() 軸左側(cè)時(shí)(如圖4),
軸左側(cè)時(shí)(如圖4),
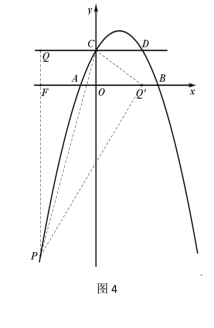
此時(shí)![]() ,
,![]() ,
,![]() =
=![]() =
=![]() ,
,
![]() =
=![]() -(
-(![]() )=
)=![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,又
,又![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]()
![]() ,
,
∴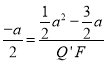 ,∴
,∴![]() ,
,
∴![]() ,
,
![]() =
=![]() =
=![]() ,
,
此時(shí)![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為(
的坐標(biāo)為(![]() ,
,![]() ).
).
綜上所述,滿足條件的點(diǎn)![]() 有兩個(gè),其坐標(biāo)分別為:(
有兩個(gè),其坐標(biāo)分別為:(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
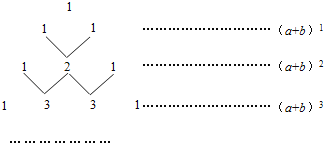
【題目】我國(guó)古代數(shù)學(xué)的許多發(fā)現(xiàn)都曾位居世界前列,其中“楊輝三角”就是一例.如圖,這個(gè)三角形的構(gòu)造法則:兩腰上的數(shù)都是1,其余每個(gè)數(shù)均為其上方左、右兩數(shù)之和,它給出了(a+b)n(n為正整數(shù))的展開式(按a的次數(shù)由大到小的順序排列)的系數(shù)規(guī)律.例如,在三角形中第三行的三個(gè)數(shù)1,2,1,恰好對(duì)應(yīng)(a+b)2=a2+2ab+b2展開式中的系數(shù);第四行的四個(gè)數(shù)1,3,3,1,恰好對(duì)應(yīng)著(a+b)3=a3+3a2b+3ab2+b2展開式中的系數(shù)等.
(1)(a+b)n展開式中項(xiàng)數(shù)共有 項(xiàng).
(2)寫出(a+b)5的展開式:(a+b)5= .
(3)利用上面的規(guī)律計(jì)算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】中華文明,源遠(yuǎn)流長(zhǎng);中華漢字,寓意深廣.為傳承中華優(yōu)秀傳統(tǒng)文化,某校團(tuán)委組織了一次全校3000名學(xué)生參加的“漢字聽寫”大賽.為了解本次大賽的成績(jī),校團(tuán)委隨機(jī)抽取了其中200名學(xué)生的成績(jī)作為樣本進(jìn)行統(tǒng)計(jì),制成如下不完整的統(tǒng)計(jì)圖表:
頻數(shù)頻率分布表
成績(jī)x(分) | 頻數(shù)(人) | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根據(jù)所給信息,解答下列問(wèn)題:
(1)m= ,n= ;
(2)補(bǔ)全頻數(shù)分布直方圖;
(3)這200名學(xué)生成績(jī)的中位數(shù)會(huì)落在 分?jǐn)?shù)段;
(4)若成績(jī)?cè)?/span>90分以上(包括90分)為“優(yōu)”等,請(qǐng)你估計(jì)該校參加本次比賽的3000名學(xué)生中成績(jī)是“優(yōu)”等的約有多少人?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,直線![]() 分別交x軸、y軸于點(diǎn)B,C,正方形AOCD的頂點(diǎn)D在第二象限內(nèi),E是BC中點(diǎn),OF⊥DE于點(diǎn)F,連結(jié)OE,動(dòng)點(diǎn)P在AO上從點(diǎn)A向終點(diǎn)O勻速運(yùn)動(dòng),同時(shí),動(dòng)點(diǎn)Q在直線BC上從某點(diǎn)Q1向終點(diǎn)Q2勻速運(yùn)動(dòng),它們同時(shí)到達(dá)終點(diǎn).
分別交x軸、y軸于點(diǎn)B,C,正方形AOCD的頂點(diǎn)D在第二象限內(nèi),E是BC中點(diǎn),OF⊥DE于點(diǎn)F,連結(jié)OE,動(dòng)點(diǎn)P在AO上從點(diǎn)A向終點(diǎn)O勻速運(yùn)動(dòng),同時(shí),動(dòng)點(diǎn)Q在直線BC上從某點(diǎn)Q1向終點(diǎn)Q2勻速運(yùn)動(dòng),它們同時(shí)到達(dá)終點(diǎn).
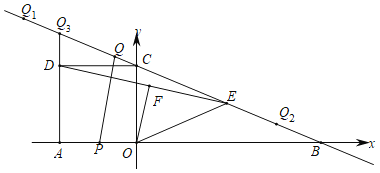
(1)求點(diǎn)B的坐標(biāo)和OE的長(zhǎng);
(2)設(shè)點(diǎn)Q2為(m,n),當(dāng)![]() tan∠EOF時(shí),求點(diǎn)Q2的坐標(biāo);
tan∠EOF時(shí),求點(diǎn)Q2的坐標(biāo);
(3)根據(jù)(2)的條件,當(dāng)點(diǎn)P運(yùn)動(dòng)到AO中點(diǎn)時(shí),點(diǎn)Q恰好與點(diǎn)C重合.
①延長(zhǎng)AD交直線BC于點(diǎn)Q3,當(dāng)點(diǎn)Q在線段Q2Q3上時(shí),設(shè)Q3Q=s,AP=t,求s關(guān)于t的函數(shù)表達(dá)式.
②當(dāng)PQ與△OEF的一邊平行時(shí),求所有滿足條件的AP的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直線![]() 軸于點(diǎn)(1,0),直線
軸于點(diǎn)(1,0),直線![]() 軸于點(diǎn)(2,0),直線
軸于點(diǎn)(2,0),直線![]() 軸于點(diǎn)(3,0),…,直線
軸于點(diǎn)(3,0),…,直線![]() 軸于點(diǎn)(n,0)。函數(shù)
軸于點(diǎn)(n,0)。函數(shù)![]() 的圖象與直線
的圖象與直線![]() 分別交于點(diǎn)
分別交于點(diǎn)![]() ;函數(shù)
;函數(shù)![]() 的圖象與直線
的圖象與直線![]() 分別交于點(diǎn)
分別交于點(diǎn)![]() 。如果
。如果![]() 的面積記作
的面積記作![]() ,四邊形
,四邊形![]() 的面積記作
的面積記作![]() ,四邊形
,四邊形![]() 的面積記作
的面積記作![]() ,…,四邊形
,…,四邊形![]() 的面積記作
的面積記作![]() ,那么
,那么![]() _____________.
_____________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司研發(fā)生產(chǎn)的560件新產(chǎn)品需要精加工后才能投放市場(chǎng).現(xiàn)由甲、乙兩個(gè)工廠來(lái)加工生產(chǎn),已知甲工廠每天加工生產(chǎn)的新產(chǎn)品件數(shù)是乙工廠每天加工生產(chǎn)新產(chǎn)品件數(shù)的1.5倍,并且加工生產(chǎn)240件新產(chǎn)品甲工廠比乙工廠少用4天.
(1)求甲、乙兩個(gè)工廠每天分別可加工生產(chǎn)多少件新產(chǎn)品?
(2)若甲工廠每天的加工生產(chǎn)成本為2.8萬(wàn)元,乙工廠每天的加工生產(chǎn)成本為2.4萬(wàn)元要使這批新產(chǎn)品的加工生產(chǎn)總成本不超過(guò)60萬(wàn)元,至少應(yīng)安排甲工廠加工生產(chǎn)多少天?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB是圓O的直徑,O為圓心,AD、BD是半圓的弦,且∠PDA=∠PBD.延長(zhǎng)PD交圓的切線BE于點(diǎn)E
(1)證明:直線PD是⊙O的切線.
(2)如果∠BED=60°,![]() ,求PA的長(zhǎng).
,求PA的長(zhǎng).
(3)將線段PD以直線AD為對(duì)稱軸作對(duì)稱線段DF,點(diǎn)F正好在圓O上,如圖2,求證:四邊形DFBE為菱形.
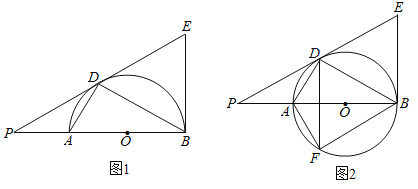
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
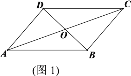
【題目】我們把有兩邊對(duì)應(yīng)相等,且?jiàn)A角互補(bǔ)(不相等)的兩個(gè)三角形叫做“互補(bǔ)三角形”,如圖1,□ABCD中,△AOB和△BOC是“互補(bǔ)三角形”.
(1)寫出圖1中另外一組“互補(bǔ)三角形”_______;
(2)在圖2中,用尺規(guī)作出一個(gè)△EFH,使得△EFH和△EFG為“互補(bǔ)三角形”,且△EFH和△EFG在EF同側(cè),并證明這一組“互補(bǔ)三角形”的面積相等.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩人在筆直的湖邊公路上同起點(diǎn)、同終點(diǎn)、同方向勻速步行2400米,先到終點(diǎn)的人原地休息.已知甲先出發(fā)4分鐘,在整個(gè)步行過(guò)程中,甲、乙兩人的距離y(米)與甲出發(fā)的時(shí)間t(分)之間的關(guān)系如圖所示,下列結(jié)論:
①甲步行的速度為60米/分;
②乙走完全程用了32分鐘;
③乙用16分鐘追上甲;
④乙到達(dá)終點(diǎn)時(shí),甲離終點(diǎn)還有300米
其中正確的結(jié)論有( )

A. 1個(gè) B. 2個(gè) C. 3個(gè) D. 4個(gè)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com