
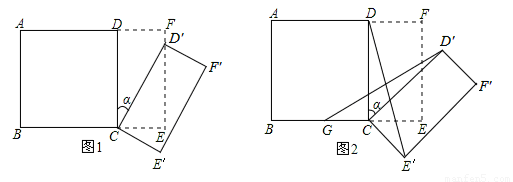
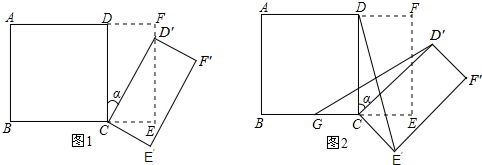
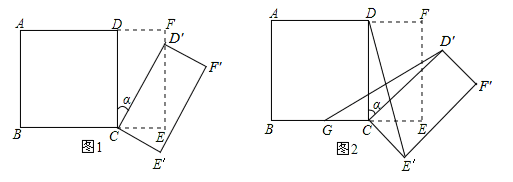
如圖1所示,將一個邊長為2的正方形ABCD和一個長為2、寬為1的長方形CEFD拼在一起,構成一個大的長方形ABEF.現將小長方形CEFD繞點C順時針旋轉至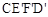 ,旋轉角為
,旋轉角為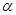 .
.
(1)當點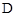 恰好落在EF邊上時,求旋轉角
恰好落在EF邊上時,求旋轉角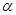 的值;
的值;
(2)如圖2,G為BC的中點,且00<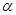 <900,求證:
<900,求證: ;
;
(3)小長方形CEFD繞點C順時針旋轉一周的過程中, 與
與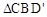 能否全等?若能,直接寫出旋轉角
能否全等?若能,直接寫出旋轉角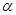 的值;若不能,說明理由.
的值;若不能,說明理由.
(1)∠α=300(2)見解析(3)旋轉角a的值為1350或3150時,△BCD′與∠DCD′全等
【解析】解:(1)∵長方形CEFD繞點C順時針旋轉至CE′F′D′,∴CD′=CD=2。
在Rt△CED′中,CD′=2,CE=1,∴sinα= 。∴∠CD′E=300。
。∴∠CD′E=300。
∵CD∥EF,∴∠α=300。
(2)證明:∵G為BC中點,BC=2,∴CG=1。∴CG=CE。
∵長方形CEFD繞點C順時針旋轉至CE′F′D′,
∴∠D′CE′=∠DCE=900,CE=CE′CE。∴∠GCD′=∠DCE′=900+α。。
在△GCD′和△∠DCE′中,
∵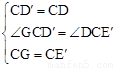 ,∴△GCD′≌△∠DCE′(SAS)。∴GD′=E′D。
,∴△GCD′≌△∠DCE′(SAS)。∴GD′=E′D。
(3)能。理由如下:
∵四邊形ABCD為正方形,∴CB=CD。
∵CD=CD′,∴△BCD′與∠DCD′為腰相等的兩等腰三角形。
當∠BCD′=∠DCD′時,△BCD′≌∠DCD。
當△BCD′與∠DCD′為鈍角三角形時, 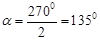 ;
;
當△BCD′與∠DCD′為銳角三角形時,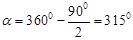 。
。
∴旋轉角a的值為1350或3150時,△BCD′與∠DCD′全等。
(1)根據旋轉的性質得CD′=CD=2,在Rt△CED′中,CD′=2,CE=1,則∠CD′E=300,然后根據平行線的性質即可得到∠α=300。
(2)由G為BC中點可得CG=CE,根據旋轉的性質得∠D′CE′=∠DCE=900,CE=CE′CE,則∠GCD′=∠DCE′=900+α,然后根據“SAS”可判斷△GCD′≌△∠DCE′,GD′=E′D。
(3)根據正方形的性質得CB=CD,而CD=CD′,則△BCD′與∠DCD′為腰相等的兩等腰三角形,當兩頂角相等時它們全等,當△BCD′與∠DCD′為鈍角三角形時,可計算出α=1350,當△BCD′與∠DCD′為銳角三角形時,可計算得到α=3150。


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(山東濰坊卷)數學(帶解析) 題型:解答題
如圖1所示,將一個邊長為2的正方形ABCD和一個長為2、寬為1的長方形CEFD拼在一起,構成一個大的長方形ABEF.現將小長方形CEFD繞點C順時針旋轉至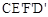 ,旋轉角為
,旋轉角為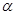 .
.
(1)當點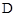 恰好落在EF邊上時,求旋轉角
恰好落在EF邊上時,求旋轉角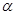 的值;
的值;
(2)如圖2,G為BC的中點,且00<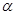 <900,求證:
<900,求證: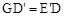 ;
;
(3)小長方形CEFD繞點C順時針旋轉一周的過程中, 與
與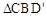 能否全等?若能,直接寫出旋轉角
能否全等?若能,直接寫出旋轉角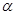 的值;若不能,說明理由.
的值;若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年河南南陽新野縣文府書院九年級第一學期期末數學試卷(解析版) 題型:解答題
如圖1所示,將一個邊長為2的正方形ABCD和一個長為2、寬為1的長方形CEFD拼在一起,構成一個大的長方形ABEF.現將小長方形CEFD繞點C順時針旋轉至CE′F′D′,旋轉角為a.
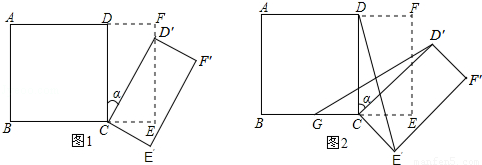
(1)當點D′恰好落在EF邊上時,求旋轉角a的值;
(2)如圖2,G為BC中點,且0°<a<90°,求證:GD′=E′D;
(3)小長方形CEFD繞點C順時針旋轉一周的過程中,△DCD′與△CBD′能否全等?若能,直接寫出旋轉角a的值;若不能說明理由.
查看答案和解析>>
科目:初中數學 來源:2013年山東省濰坊市中考數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com