
武漢一橋維修工程中,擬由甲、乙兩各工程隊共同完成某項目,從兩個工程隊的資料可以知道,若兩個工程隊合作24天恰好完成,若兩個工程隊合作18天后,甲工程隊再單獨做10天,也恰好完成,請問:
⑴甲、乙兩工程隊完成此項目各需多少天?
⑵又已知甲工程隊每天的施工費用是0.6萬元,乙工程隊每天的施工費用是0.35萬元,要使該項目總的施工費用不超過22萬元,則乙工程隊至少施工多少天?
⑴甲、乙兩工程隊單獨完成此項目分別需40天、60天;
⑵乙工程度至少要施工40天.
【解析】
試題分析:(1)本題是一個有關于二元一次的分式方程.若兩個工程隊合作24天恰好完成;若兩個工程隊合作18天后,甲工程隊再單獨做10天,也恰好完成.可得出兩個等量關系:甲24天完成工作量+乙24天工作量=1;甲乙合作18天的工作量+甲單獨做10天的工作量=1,由此可列出方程組求解.
(2)可由甲乙兩隊的工作量之和為1及總費用不超過22萬元兩個關系進行分析.
⑴設甲工程隊單獨完成該項目需要 天,乙單獨完成該項目需要
天,乙單獨完成該項目需要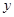 天,
天,
依題意可列方程組為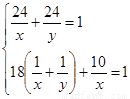 ,解得
,解得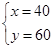 ,
,
經檢驗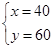 是原方程組的解,也符合題意;
是原方程組的解,也符合題意;
⑵設甲、乙兩工程隊分別施工a天、b天,由于總施工費用不超過22萬元,
可得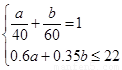 ,解得
,解得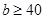 ,b取最小值為40.
,b取最小值為40.
故⑴甲、乙兩工程隊單獨完成此項目分別需40天、60天;⑵乙工程度至少要施工40天.
考點:本題考查分式方程的應用
點評:列方程解應用題的步驟是:一審(審題)二設(設出相應未知數)三列(根據等量關系和所設未知數列出方程)四解(解方程)五檢驗(檢驗是否是方程的解,是否符合實際問題含義)六回答(根據所問的進行回答),其中審題時找出等量關系是列方程解決實際問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:
武漢江漢一橋維修工程中,擬由甲、乙兩個工程隊共同完成某項目。從兩個工程隊的資料可以知道:若兩個工程隊合做24天恰好完成;若兩個工程隊合做18天后,甲工程隊再單獨做10天,也恰好完成。請問:
(1)甲、乙兩個工程隊單獨完成該項目各需多少天?
(2)又已知甲工程隊每天的施工費為0.6萬元,乙工程隊每天的施工費為0.35萬元,要使該項目總的施工費不超過22萬元,則乙工程隊最少施工多少天?
查看答案和解析>>
科目:初中數學 來源:湖南省同步題 題型:解答題
查看答案和解析>>
科目:初中數學 來源:同步題 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com