
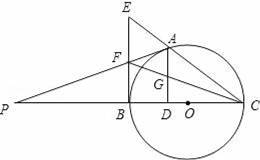
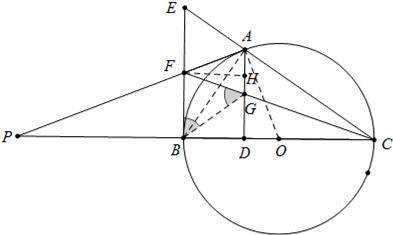
如圖,點A是以BC為直徑的⊙O上一點,AD⊥BC于點D,過點B作⊙O的切線,與CA的延長線相交于點E,G是AD的中點,連結CG并延長與BE相交于點F,延長AF與CB的延長線相交于點P,且FG=FB=3.則以下四個結論:①BF=EF;②PA⊥OA;③tan∠P=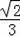
 ;④OC=3
;④OC=3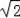
 ,上述結論中正確的有 (填番號).
,上述結論中正確的有 (填番號).

①②④ (填番號).
【考點】圓的綜合題.
【分析】①正確,根據(jù)AD∥EB得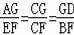
 即可證明.②正確,只要證明∠FAB+∠OAB=90°即可.③錯誤,求出AH,F(xiàn)H,根據(jù)tan∠P=tan∠AFH=
即可證明.②正確,只要證明∠FAB+∠OAB=90°即可.③錯誤,求出AH,F(xiàn)H,根據(jù)tan∠P=tan∠AFH=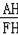
 =
=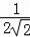
 =
=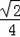
 ,即可解決問題.④正確,在RT△ADO中利用勾股定理即可求出半徑.
,即可解決問題.④正確,在RT△ADO中利用勾股定理即可求出半徑.
【解答】解:如圖連接AO、AB、BG作FH⊥AD于H,
∵EB是切線,AD⊥BC
∴∠EBC=∠ADC=90°,
∴AD∥EB,
∴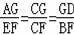
 ,
,
∵AG=GD,
∴EF=FB故①正確,
∵BC是直徑,
∴∠BAC=∠BAE=90°,∵EF=FB,
∴FA=FB=FE=FG=3,
∴∠FAB=∠FBA,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FBA+∠ABO=90°,
∴∠FAB+∠OAB=90°,
∴PA是⊙O的切線,故②正確.
∵FA=FG,F(xiàn)H⊥AG,
∴AH=HG,
∵∠FBD=∠BDH=∠FHD=90°,
∴四邊形FBDH是矩形,
∴FB=DH=3,
∵AG=GD,
∴AH=HG=1,GD=2,F(xiàn)H=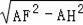
 =2
=2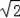
 ,
,
∵FH∥PD,
∴∠AFH=∠APD,
∴tan∠P=tan∠AFH=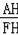
 =
=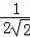
 =
=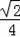
 ,故③錯誤,
,故③錯誤,
設半徑為r,在RT△ADO中,∵AO2=AD2+OD2,
∴r2=42+(r﹣2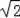
 )2,
)2,
∴r=3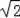
 故④正確,
故④正確,
故答案為①②④.

【點評】本題考查圓的有關知識、平行線分線段成比例定理、直角三角形斜邊中線定理、勾股定理等知識,解題的關鍵是添加常用輔助線,體現(xiàn)了轉化的思想,把問題轉化為方程解決,屬于中考壓軸題.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數(shù)學 來源: 題型:
在某次體育測試中,九年級一班女同學的一分鐘仰臥起坐成績(單位:個)如下表:
| 成績 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人數(shù) | 1 | 2 | 4 | 2 | 5 | 1 |
這此測試成績的中位數(shù)和眾數(shù)分別為( )
A.47,49 B.47.5,49 C.48,49 D.48,50
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
下列現(xiàn)象:①電梯的升降運動,②飛機在地面上沿直線滑行,③風車的轉動,④冷水加熱過程中氣泡的上升.其中屬于平移的是( )
A.①② B.①③ C.②③ D.③④
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
如圖,線段AB兩個端點的坐標分別為A(6,6),B(8,2),以原點O為位似中心,在第一象限內將線段AB縮小為原來的
 后得到線段CD,則端點C的坐標為( )
后得到線段CD,則端點C的坐標為( )
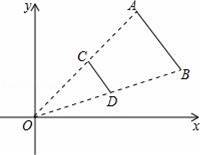

A.(3,3) B.(4,3) C.(3,1) D.(4,1)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
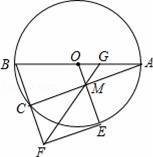
如圖,⊙O是△ABC的外接圓,AB為直徑,過點O作OM∥BC,交AC于點M.
(1)求∠AMO;
(2)延長OM交⊙O于點E,過E作⊙O的切線,交BC延長線于點F,連接FM,并延長FM交AB于點G.
①試判斷四邊形CFEM的形狀,并說明理由;
②若AG=2,CM=3,求四邊形CFEM的面積.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
小明參加某網(wǎng)店的“翻牌抽獎”活動,如圖,4張牌分別對應價值5,10,15,20(單位:元)的4件獎品.
(1)如果隨機翻1張牌,那么抽中20元獎品的概率為
(2)如果隨機翻2張牌,且第一次翻過的牌不再參加下次翻牌,則所獲獎品總值不低于30元的概率為多少?


查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com