
【題目】在菱形![]() 中,
中,![]() ,
,![]() 是對角線
是對角線![]() 上一點,
上一點,![]() 是線段
是線段![]() 延長線上一點,且
延長線上一點,且![]() ,連接
,連接![]() 、
、![]() .
.
![]() 若
若![]() 是線段
是線段![]() 的中點,如圖
的中點,如圖![]() ,易證:
,易證:![]() (不需證明);
(不需證明);
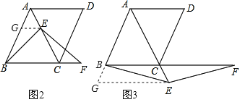
![]() 若
若![]() 是線段
是線段![]() 或
或![]() 延長線上的任意一點,其它條件不變,如圖
延長線上的任意一點,其它條件不變,如圖![]() 、圖
、圖![]() ,線段
,線段![]() 、
、![]() 有怎樣的數量關系,直接寫出你的猜想;并選擇一種情況給予證明.
有怎樣的數量關系,直接寫出你的猜想;并選擇一種情況給予證明.

【答案】(1)見解析;(2)![]() .
.
【解析】
(1)根據菱形的性質結合∠ABC=60°可得△ABC是等邊三角形,再根據等腰三角形三線合一的性質可得∠CBE=![]() ∠ABC=30°,AE=CE,所以CE=CF,然后等邊對等角的性質可得∠F=∠CEF,根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠F=30°,從而得到∠CBE=∠F,根據等角對等邊的性質即可證明;
∠ABC=30°,AE=CE,所以CE=CF,然后等邊對等角的性質可得∠F=∠CEF,根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠F=30°,從而得到∠CBE=∠F,根據等角對等邊的性質即可證明;
(2)圖2,過點E作EG∥BC,交AB于點G,根據菱形的性質結合∠ABC=60°可得△ABC是等邊三角形,然后根據等邊三角形的性質得到AB=AC,∠ACB=60°,再求出△AGE是等邊三角形,根據等邊三角形的性質得到AG=AE,從而可以求出BG=CE,再根據等角的補角相等求出∠BGE=∠ECF=120°,然后利用“邊角邊”證明△BGE和△ECF 全等,根據全等三角形對應邊相等即可得證;圖3,證明思路與方法與圖2完全相同.
![]() ∵四邊形
∵四邊形![]() 為菱形,
為菱形,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∵![]() 是線段
是線段![]() 的中點,
的中點,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 圖
圖![]() .
.
圖![]() .
.
圖![]() 證明如下:過點
證明如下:過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,
,
∵四邊形![]() 為菱形,
為菱形,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,![]() ,…
,…
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等邊三角形,…
是等邊三角形,…
∴![]() ,
,
∴![]() ,…
,…
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
圖![]() 證明如下:過點
證明如下:過點![]() 作
作![]() 交
交![]() 延長線于點
延長線于點![]() ,
,
∵四邊形![]() 為菱形,
為菱形,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
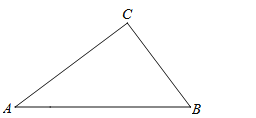
【題目】如圖,△ABC中,AB=5cm,BC=3cm,AC=4cm,若動點P從點C開始,按照C→A→B的路徑運動,且運動速度為每秒2cm,設出發的時間為t秒.
(1)請判斷△ABC的形狀,說明理由
(2)當t為何值時,△BCP是以BC為腰的等腰三角形,求出t的值
(3)另有一點Q,從點C開始,按C→B→A→C的路徑運動,且速度為每秒1cm,若P、Q兩點同時出發, 當P、Q中有一點到達終點時,另一點也停止運動,當t為何值時,P、Q兩點之間的距離為![]() ,直接寫出t的值.
,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級某班同學在慶祝2015年元旦晚會上進行抽獎活動.在一個不透明的口
袋中有三個完全相同的小球,把它們分別標號1、2、3.隨機摸出一個小球記下標號后放回搖勻,再從中隨
機摸出一個小球記下標號.
(1)請用列表或畫樹形圖的方法(只選其中一種),表示兩次摸出小球上的標號的所有結果;
(2)規定當兩次摸出的小球標號相同時中獎,求中獎的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
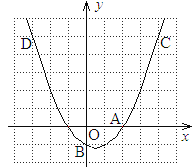
【題目】如圖,已知二次函數![]() 的圖象過A(2,0),B(0,-1)和C(4,5)三點。
的圖象過A(2,0),B(0,-1)和C(4,5)三點。
(1)求二次函數的解析式;
(2)設二次函數的圖象與![]() 軸的另一個交點為D,求點D的坐標;
軸的另一個交點為D,求點D的坐標;
(3)在同一坐標系中畫出直線![]() ,并寫出當
,并寫出當![]() 在什么范圍內時,一次函數的值大于二次函數的值。
在什么范圍內時,一次函數的值大于二次函數的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
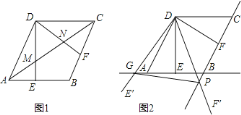
【題目】如圖![]() ,菱形
,菱形![]() 對角線
對角線![]() 、
、![]() 的交點
的交點![]() 是四邊形
是四邊形![]() 對角線
對角線![]() 的中點,四個頂點
的中點,四個頂點![]() 、
、![]() 、
、![]() 、
、![]() 分別在四邊形
分別在四邊形![]() 的邊
的邊![]() 、
、![]() 、
、![]() 、
、![]() 上.
上.
![]() 求證:四邊形
求證:四邊形![]() 是平行四邊形;
是平行四邊形;
![]() 如圖
如圖![]() 若四邊形
若四邊形![]() 是矩形,當
是矩形,當![]() 與
與![]() 重合時,已知
重合時,已知![]() ,且菱形
,且菱形![]() 的面積是
的面積是![]() ,求矩形
,求矩形![]() 的長與寬.
的長與寬.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,![]() 于點
于點![]() .
.
![]() 如圖
如圖![]() ,連接
,連接![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,求證:
,求證:![]() ;
;
![]() 如圖
如圖![]() ,將
,將![]() 以點
以點![]() 為旋轉中心旋轉,其兩邊
為旋轉中心旋轉,其兩邊![]() 、
、![]() 分別與直線
分別與直線![]() 、
、![]() 相交于點
相交于點![]() 、
、![]() ,連接
,連接![]() ,當
,當![]() 的面積等于
的面積等于![]() 時,求旋轉角的大小并指明旋轉方向.
時,求旋轉角的大小并指明旋轉方向.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com