為了抓住國家降低汽車購置稅,刺激汽車消費的大好機遇,實現新的發展,汽車生產企業策劃部擬定了以下兩種新的投資方案.方案一:生產家用型汽車,每輛汽車成本為a萬元(a為常數,且3<a<8),每輛汽車銷售價為10萬元,每年最多可生產200輛;方案二:生產豪華型汽車,每輛汽車成本為8萬元,每輛汽車銷售價為18萬元,每年最多可生產120輛.假設生產汽車的輛數為x(x為正整數),且生產的汽車可全部售出,又已知年銷售x輛豪華型汽車時需上交0.05x2萬元的附加稅.在不考慮其他因素的情況下:
(1)分別寫出該企業兩個投資方案的年利潤y1、y2與生產汽車輛數x之間的函數關系式,并指出自變量的取值范圍;
(2)分別求出這兩個投資方案的最大年利潤;
(3)如果你是企業決策者,為了獲得最大收益,你會選擇哪種投資方案?
【答案】
分析:(1)利用汽車的輛數乘以每輛的利潤,即售價與成本的差,即可求得;
(2)根據兩個函數的性質求兩個函數的最大值即可;
(3)根據(2)中得到的利潤的值,進行比較,求得a的范圍,從而根據a的值確定選擇哪種方案.
解答:解:(1)y
1=(10-a)x (0≤x≤200)
y
2=10x-0.05x
2 (0≤x≤120)
(2)方案一:∵10-a>0,則當x=200時,年利潤最大,是200(10-a);
方案二:x=-
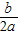
=-
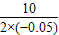
=100,則當x=100時,利潤最大,是:10×100-0.05×100
2=500(萬元).
(3)當200(10-a)>500時,a<7.5,則3<a<7.5時,選擇方案一;
當200(10-a)=500時,a=7.5,兩種方案相同;
當200(10-a)<500時,a>7.5,則7.5<a<8時,選擇方案二.
點評:此題屬于一次函數的應用題,考查數列模型的構建,考查利用數學知識解決實際問題,解題的構建是確定數列模型.

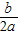 =-
=-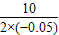 =100,則當x=100時,利潤最大,是:10×100-0.05×1002=500(萬元).
=100,則當x=100時,利潤最大,是:10×100-0.05×1002=500(萬元).
