
(13分)如圖,在△ABC中,∠ACB=90°,CD⊥AB,

(1)圖中共有 對相似三角形,寫出來分別為 (不需證明);
(2)已知AB=10,AC=8,請你求出CD的長;
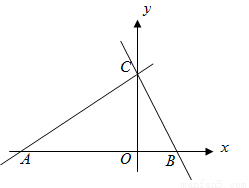
(3)在(2)的情況下,如果以AB為x軸,CD為y軸,點D為坐標原點O,建立直角坐標系(如下圖),若點P從C點出發,以每秒1個單位的速度沿線段CB運動,點Q出B點出發,以每秒1個單位的速度沿線段BA運動,其中一點最先到達線段的端點時,兩點即刻同時停止運動;設運動時間為 秒是否存在點P,使以點B、P、Q為頂點的三角形與△ABC相似?若存在,請求出點
秒是否存在點P,使以點B、P、Q為頂點的三角形與△ABC相似?若存在,請求出點 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(1)3對,分別是:△ABC∽△ACD, △ABC∽△CBD , △ACD∽△CBD;(2)4.8;(3)存在,(1.35,3)或(3.15,1.8).
【解析】
試題分析:(1)根據兩角對應相等的兩三角形相似即可得到3對相似三角形,分別為:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)先在△ABC中由勾股定理求出BC的長,再根據△ABC的面積不變得到 AB•CD=
AB•CD= AC•BC,即可求出CD的長;
AC•BC,即可求出CD的長;
(3)由于∠B公共,所以以點B、P、Q為頂點的三角形與△ABC相似時,分兩種情況進行討論:①△PQB∽△ACB;②△QPB∽△ACB.
試題解析:(1)圖1中共有3對相似三角形,分別為:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案為3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如圖1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,∴BC= =6.
=6.
∵△ABC的面積= AB•CD=
AB•CD= AC•BC,∴CD=
AC•BC,∴CD= =4.8;
=4.8;
(3)存在點P,使以點B、P、Q為頂點的三角形與△ABC相似,理由如下:在△BOC中,∵∠COB=90°,BC=6,OC=4.8,∴OB= =3.6.
=3.6.
分兩種情況:①當∠BQP=90°時,如圖2①,此時△PQB∽△ACB,
∴ ,∴
,∴ ,解得t=2.25,即BQ=CP=2.25,
,解得t=2.25,即BQ=CP=2.25,
∴OQ=OB﹣BQ=3.6﹣2.25=1.35,BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ= =
= ,∴點P的坐標為(1.35,3);
,∴點P的坐標為(1.35,3);

②當∠BPQ=90°時,如圖2②,此時△QPB∽△ACB,∴ ,∴
,∴ ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
過點P作PE⊥x軸于點E.
∵△QPB∽△ACB,∴ ,∴
,∴ ,∴PE=1.8.
,∴PE=1.8.
在△BPE中,BE= =
= ,∴OE=OB﹣BE=3.6﹣0.45=3.15,
,∴OE=OB﹣BE=3.6﹣0.45=3.15,
∴點P的坐標為(3.15,1.8);
綜上可得,點P的坐標為(1.35,3)或(3.15,1.8).

考點:1.相似三角形的判定與性質;2.勾股定理.


科目:初中數學 來源:2014-2015學年福建省南平市八年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖所示,亮亮書上的三角形被墨跡污染了一部分,很快他就根據所學知識畫出一個與書上完全一樣的三角形,那么這兩個三角形完全一樣的依據是( )

A.SSS B.SAS C.AAS D.ASA
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省泉州市惠安第三教研片區九年級上學期期中考試數學試卷(解析版) 題型:選擇題
若二次根式 有意義,則
有意義,則 的取值范圍是( )
的取值范圍是( )
A. B.
B.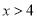 C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省泉州市惠安第三教研片區九年級上學期期中考試數學試卷(解析版) 題型:填空題
已知△ABC與△DEF相似且相似比為2:3,則△ABC與△DEF的面積比是________.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省漳州立人學校八年級上學期期中考試數學試卷(解析版) 題型:選擇題
下列是有理數的是( )
A.0
B.
C.
D.1.010010001…(每兩個1之間的0的個數依次多1)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省漳州立人學校八年級上學期期中考試數學試卷(解析版) 題型:解答題
如圖,△ABC的頂點坐標分別是A(2,2)、B(3,5)、C(6,1)

(1)作△A′B′C′,使△ABC與△A′B′C′關于x軸對稱;
(2)AB長度是 (填“有理數”或“無理數”) ,BC= ;
(3)△ABC 直角三角形(填“是”或“不是”);
(4)△ABC的面積= 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com