
【題目】如圖①所示,已知正方形ABCD和正方形AEFG,G、A、B在同一直線上,點E在AD上,連接DG,BE.
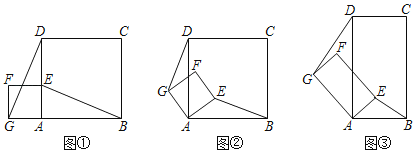
(1)證明:BE=DG;
(2)發現:當正方形AEFG繞點A旋轉,如圖②所示,判斷BE與DG的數量關系和位置關系,并說明理由;
(3)探究:如圖③所示,若四邊形ABCD與四邊形AEFG都為矩形,且AD=2AB,AG=2AE時,判斷BE與DG的數量關系和位置關系是否與(2)的結論相同,并說明理由.
【答案】(1)證明見解析;(2)BE=DG,BE⊥DG,理由見解析;(3)數量關系不成立即BE≠DG,DG=2BE,理由見解析;位置關系成立,理由見解析
【解析】
(1)根據正方形的性質及全等三角形的判定可得△ABE≌△DAG(SAS),再根據全等三角形的性質即可得出結論;
(2)根據正方形的性質可知:AE=AG,AB=AD,∠BAD=∠EAG=90°,再根據同腳的余角相等得出∠BAE=∠DAG,然后根據全等三角形的判定定理得出△ABE≌△DAG(SAS)再由全等三角形的性質定理可得出BE=DG,∠ABE=∠ADG;延長BE交AD于T,交DG于H.進而得出∠DHB=90°,即BE⊥DG.
(3)根據四邊形ABCD和四邊形AEFG都是矩形,且AD=2AB,AG=2AE時,則△ABE∽△ADG,再根據相似三角形的性質即可得出結論.
解:(1)證明:∵四邊形ABCD和四邊形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴△ABE≌△DAG(SAS),
∴BE=DG;
(2)BE=DG,BE⊥DG.
如圖1中,∵四邊形ABCD和四邊形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△DAG中,
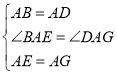 ,
,
∴△ABE≌△DAG(SAS),
∴BE=DG;∠ABE=∠ADG,
延長BE交AD于T,交DG于H.

∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG.
(3)數量關系不成立,它們的數量關系為DG=2BE,位置關系成立.
如圖2中,延長BE交AD于T,交DG于H.
∵四邊形ABCD與四邊形AEFG都為矩形,
∴∠BAD=∠DAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴![]() ,
,
∴△ABE∽△ADG,
∴∠ABE=∠ADG,![]() ,
,
∴DG=2BE,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG.


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:
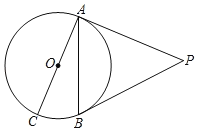
【題目】如圖,PA,PB是⊙O的切線,A,B為切點,AC是⊙O的直徑.
(1)若∠BAC=25°,求∠P的度數;
(2)若∠P=60°,PA=2![]() ,求AC的長.
,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位計劃從商店購買同一種品牌的鋼筆和筆記本,已知購買一支鋼筆比購買一個筆記本多用20元,若用1500元購買鋼筆和用600元購買筆記本,則購買鋼筆的數量是購買筆記本數量的一半.
(1)求購買一支鋼筆、一個筆記本各需要多少元?
(2)經商談,商店給予優惠,優惠方式是每購買一支鋼筆贈送一個筆記本;如果此單位需要筆記本的數量是鋼筆數量的3倍還少6個,且購買鋼筆和筆記本的總費用不超過1020元,那么最多可購買多少支鋼筆?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,∠ACB=30°,將△ABC繞點C順時針旋轉60°得到△DEC,點A、B的對應點分別是D、E,點F是邊AC中點,①△BCE是等邊三角形,②DE=BF,③△ABC≌△CFD,④四邊形BEDF是平行四邊形.則其中正確結論的個數是( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
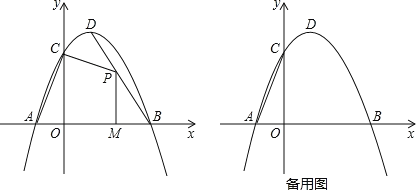
【題目】如圖,在平面直角坐標系中,拋物線y=﹣ax2+bx+3與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于點C,點D是該拋物線的頂點.
(1)求直線AC及拋物線的解析式,并求出D點的坐標;
(2)若P為線段BD上的一個動點,過點P作PM⊥x軸于點M,求四邊形PMAC的面積的最大值和此時點P的坐標;
(3)若點P是x軸上一個動點,過P作直線1∥AC交拋物線于點Q,試探究:隨著P點的運動,在拋物線上是否存在點Q,使以點A、P、Q、C為頂點的四邊形是平行四邊形?若存在,請求出符合條件的點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年12月以來,湖北省武漢市部分醫院陸續發現不明原因肺炎病例,現已證實該肺炎為一種新型冠狀病毒感染的肺炎,其傳染性較強.為了有效地避免交叉感染,需要采取以下防護措施:①戴口罩;②勤洗手;③少出門;④重隔離;⑤捂口鼻;⑥謹慎吃.某公司為了解員工對防護措施的了解程度(包括不了解、了解很少、基本了解和很了解),通過網上問卷調查的方式進行了隨機抽樣調查(每名員工必須且只能選擇一項),并將調查結果繪制成如下兩幅統計圖.
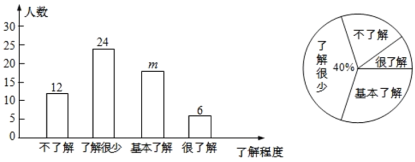
請你根據上面的信息,解答下列問題
(1)本次共調查了_______名員工,條形統計圖中![]() ________;
________;
(2)若該公司共有員工1000名,請你估計不了解防護措施的人數;
(3)在調查中,發現有4名員工對防護措施很了解,其中有3名男員工、1名女員工.若準備從他們中隨機抽取2名,讓其在公司群內普及防護措施,求恰好抽中一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
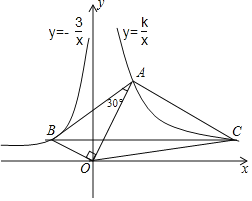
【題目】如圖,已知∠AOB=90°,∠OAB=30°,反比例函數![]() 的圖象過點
的圖象過點![]() ,反比例函數
,反比例函數![]() 的圖象過點A
的圖象過點A
(1)求![]() 和
和![]() 的值.
的值.
(2)過點B作BC∥x軸,與雙曲線![]() 交于點C,求△OAC的面積.
交于點C,求△OAC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用四塊大正方形地磚和一塊小正方形地磚拼成如圖所示的實線圖案,每塊大正方形地磚面積為a,小正方形地磚面積為依次連接四塊大正方形地磚的中心得到正方形ABCD.則正方形ABCD的面積為____________(用含a,b的代數式表示).
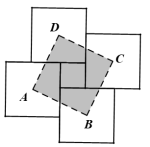
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數y1的圖象與反比例函數y2的圖象相交于點A(2,-4),下列說法正確的是( )
A.反比例函數y2的解析式是![]()
B.兩個函數圖象的另一交點坐標為(2,4)
C.當x<-2或0<x<2時,y1>y2
D.正比例函數y1與反比例函數y2都隨x的增大而減小
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com