
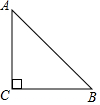
 如圖,△ABC中,∠C=90°,CA=CB=1,將△ABC繞點B順時針旋轉45°,得到△DBE(A、D兩點為對應點),畫出旋轉后的圖形,并求出線段AE的長.
如圖,△ABC中,∠C=90°,CA=CB=1,將△ABC繞點B順時針旋轉45°,得到△DBE(A、D兩點為對應點),畫出旋轉后的圖形,并求出線段AE的長. 分析 在BA上截取BE=BC,過點B作DB⊥BC,且DB=AB,則連接DE得到△DBE,再利用等腰三角形的性質得到∠ABC=45°,AB=$\sqrt{2}$BC=$\sqrt{2}$,利用旋轉的性質得到∠CBE=45°,BC=BE=1,于是可判斷點E在AB上,所以AE=AB-BE=$\sqrt{2}$-1.
解答 解:如圖,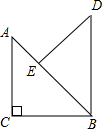
∵∠C=90°,CA=CB=1,
∴∠ABC=45°,AB=$\sqrt{2}$BC=$\sqrt{2}$,
∵△ABC繞點B順時針旋轉45°,得到△DBE,
∴∠CBE=45°,BC=BE=1,
∵∠CBE=∠CBA,
∴點E在AB上,
∴AE=AB-BE=$\sqrt{2}$-1.
點評 本題考查了作圖-旋轉變換:根據旋轉的性質可知,對應角都相等都等于旋轉角,對應線段也相等,由此可以通過作相等的角,在角的邊上截取相等的線段的方法,找到對應點,順次連接得出旋轉后的圖形.也考查了等腰直角三角形的性質.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:解答題
 如圖,一居民樓底部B與山腳P位于同一水平線上,小李在P處測得居民樓頂A的仰角為60°,然后他從P處沿坡腳為45°的上坡向上走到C處,這時,PC=20$\sqrt{2}$m,點C與點A在同一水平線上,A、B、P、C在同一平面內.
如圖,一居民樓底部B與山腳P位于同一水平線上,小李在P處測得居民樓頂A的仰角為60°,然后他從P處沿坡腳為45°的上坡向上走到C處,這時,PC=20$\sqrt{2}$m,點C與點A在同一水平線上,A、B、P、C在同一平面內.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
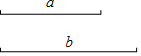 已知:線段a,b.
已知:線段a,b.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
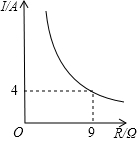 已知蓄電池的電壓U為定值,使用蓄電池時,電流I(單位:A)與電阻R(單位:Ω)是反比例函數關系,它的圖象如圖所示.
已知蓄電池的電壓U為定值,使用蓄電池時,電流I(單位:A)與電阻R(單位:Ω)是反比例函數關系,它的圖象如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系中,對于任意一點P(x,y),我們做以下規定:d(P)=|x|+|y|,稱d(P)為點P的坐標距離.
在平面直角坐標系中,對于任意一點P(x,y),我們做以下規定:d(P)=|x|+|y|,稱d(P)為點P的坐標距離.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com