
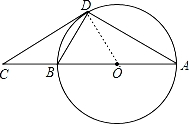
如圖,點C是⊙O的直徑AB延長線上的一點,且有BO=BD=BC.
(1)求證:CD是⊙O的切線;
(2)若半徑OB=2,求AD的長.

【考點】切線的判定;含30度角的直角三角形;勾股定理.
【專題】證明題.
【分析】(1)由于BO=BD=BC,即DB為△ODC的邊OC的中線,且有DB=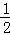 OC,則∠ODC=90°,然后根據切線的判定方法即可得到結論;
OC,則∠ODC=90°,然后根據切線的判定方法即可得到結論;
(2)由AB為⊙O的直徑得∠BDA=90°,而BO=BD=2,則AB=2BD=4,然后根據勾股定理可計算出AD.
【解答】(1)證明:連結OD,如圖,
∵BO=BD=BC,
∴BD為△ODC的中線,且DB=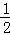 OC,
OC,
∴∠ODC=90°,
∴OD⊥CD,
而OD為⊙O的半徑,
∴CD是⊙O的切線;
(2)解:∵AB為⊙O的直徑,
∴∠BDA=90°,
∵BO=BD=2,
∴AB=2BD=4,
∴AD=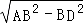 =2
=2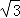 .
.
【點評】本題考查了切線的判定定理:過半徑的外端點且與半徑垂直的直線為圓的切線.也考查了直角三角形的判定方法、勾股定理.


 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:
一個盒子內裝有大小、形狀相同的四個球,其中紅球1個、綠球1個、白球2個,小明摸出一個球不放回,再摸出一個球,則兩次都摸到白球的概率是( )
A.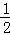 B.
B. C.
C.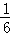 D.
D.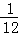
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,邊長為(m+3)的正方形紙片,剪出一個邊長為m的正方形之后,剩余部分可剪拼成一個矩形(不重疊無縫隙),若拼成的矩形一邊長為3,則另一邊長是( )


A.m+3 B.m+6 C.2m+3 D.2m+6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com