
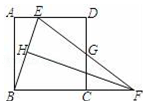
【題目】如圖,在正方形ABCD中,點E是AD上的點,點F是BC的延長線上一點,CF=DE,連結BE和EF,EF與CD交于點G,且∠FBE=∠FEB.
(1)過點F作FH⊥BE于點H,證明: ![]() =
= ![]() ;
;
(2)猜想:BE、AE、EF之間的數量關系,并證明你的結論;
(3)若DG=2,求AE值.
【答案】
(1)
證明:∵在正方形ABCD中,AD∥BC,
∴∠AEB=∠EBF,
又∵FH⊥BE,
∴∠A=∠BHF=90°,
∴△ABE∽△HFB,
∴ ![]() =
= ![]()
(2)
BE2=2AEEF,
證明如下:∵∠FBE=∠FEB,
∴BF=EF,
∵FH⊥BE,
∴FH是等腰△FBE底邊上的中線,
∴BH= ![]() BE,
BE,
由(1)得, ![]() ,
,
∴ ![]()
∴BE2=2AEBF;
∵BF=EF,
∴BE2=2AEEF
(3)
解:∵DG═2,
∴正方形ABCD的邊長為4,
設AE=k(0<k<4),
則DE═4﹣k,BF=8﹣k,
在Rt△ABM中,BE2=AB2+AE2=16+k2,
由BE2=2AEBF,得16+k2=2k(8﹣k),
即3k2﹣16k+16=0,解得 k= ![]() 或k=4
或k=4
∵k≠4,
∴AE= ![]()
【解析】(1)根據正方形的性質得到∠AEB=∠EBF,由已知條件得到∠A=∠BHF,根據相似三角形的判定定理即可得到結論;(2)根據已知條件得到FH是等腰△FBE底邊上的高,求得BH= ![]() BE,由根據相似三角形的性質得到
BE,由根據相似三角形的性質得到 ![]() ,等量代換即可得到結論;(3)由已知條件得到正方形ABCD的邊長為4,設AE=k(0<k<2),則DE═4﹣k,BF=8﹣k,根據勾股定理列方程即可得到結果.
,等量代換即可得到結論;(3)由已知條件得到正方形ABCD的邊長為4,設AE=k(0<k<2),則DE═4﹣k,BF=8﹣k,根據勾股定理列方程即可得到結果.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】2018年在中央“房子是用來住的,不是用來炒”的精神作用下,房子價格持續下跌.玲玲家買了一套新房準備裝修,若甲、乙兩個裝飾公司合作,需6周完成,共需裝修費為5.2萬元;若甲公司單獨做4周后,剩下的由乙公司來做,還需9周才能完成,共需裝修費為4.8萬元.玲玲的爸爸媽媽商量后決定只選一個公司單獨完成.
(1)如果從節約時間的角度考慮應選哪家公司?
(2)如果從節約開支的角度考慮應選哪家公司?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某條道路上通行車輛限速為60千米/時,在離道路50米的點P處建一個監測點,道路AB段為檢測區(如圖).在△ABP中,已知∠PAB=30°,∠PBA=45°,一輛轎車通過AB段的時間8.1秒,請判斷該車是否超速?(參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/時=
≈1.73,60千米/時= ![]() 米/秒)
米/秒) 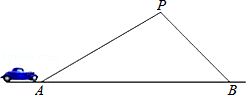
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家生產的一種新型節能燈,為了打開市場出臺了相關政策:由廠家協調,廠家按成本價提供產品給經營戶自主銷售,成本價與出廠價之間的差價由廠家承擔.李明按照相關政策投資銷售本產品.已知這種節能燈的成本價為每件10元,出廠價為每件12元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=﹣10x+500.
(1)李明在開始銷售的第一個月將銷售單價定為20元,那么廠家這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3000元,那么廠家為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB>AC,點D、E分別是邊AB、AC的中點,點F在BC邊上,連接DE、DF、EF,則添加下列哪一個條件后,仍無法判斷△FCE與△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃購買一批籃球和足球,已知購買2個籃球和1個足球共需320元,購買3個籃球和2個足球共需540元.
(1)求每個籃球和每個足球的售價;
(2)如果學校計劃購買這兩種球共50個,總費用不超過5500元,那么最多可購買多少個足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD沿AH折疊,使得頂點B落在CD邊上的P點處.折痕與邊BC交于點 H,已知AD=8,HC:HB=3:5.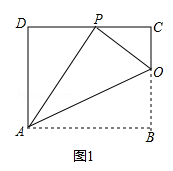
(1)求證:△HCP∽△PDA;
(2)探究AB與HB之間的數量關系,并證明你的結論;
(3)連結BP,動點M在線段AP上(點M與點P、A不重合),動點N在線段AB的延長線上,且BN=PM,連結MN交PB于點F,作ME⊥BP于點E.試問當點M、N在移動過程中,線段EF的長度是否發生變化?若變化,說明理由;說明理由;若不變,求出線段EF的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com