Question

10．平面直角坐標系中，A（8，0），△AOP為等腰三角形且面積為16，滿足條件的第二象限內的點P坐標（-4$\sqrt{3}$，4）．

Answer 1

分析 使△AOP為等腰三角形，只需分兩種情況考慮：OA當底邊或OA當腰．當OA是底邊時，有2個點；當OA是腰時，有8個點，即可得出答案．

解答 解：∵A（8，0），
∴OA=8，
設△AOP的邊OA上的高是h，
則$\frac{1}{2}$×8×h=16，
解得：h=4，
在x軸的兩側作直線a和直線b都和x軸平行，且到x軸的距離都等于4，如圖：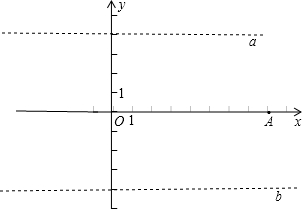

①以A為圓心，以8為半徑畫弧，交直線a和直線b分別有兩個點，即共4個點符合，
②以O為圓心，以8為半徑畫弧，交直線a和直線b分別有兩個點，即共4個點符合，
③作AO的垂直平分線分別交直線a、b于一點，即共2個點符合，
4+4+1+1=10．
滿足條件的第二象限內的點P坐標為（-4$\sqrt{3}$，4）
故答案為：（-4$\sqrt{3}$，4）

點評 此題主要考查了坐標與圖形的性質及等腰三角形的判定；對于底和腰不等的等腰三角形，若條件中沒有明確哪邊是底哪邊是腰時，應在符合三角形三邊關系的前提下分類討論．