
【題目】如圖,△ABC和△ADE是有公共頂點的等腰直角三角形,∠BAC=∠DAE=90°,點P為直線BD,CE的交點.
(1)如圖,將△ADE繞點A旋轉,當D在線段CE上時,連接BE,下列給出兩個結論:①BD=CD+![]() AD;②BE2=2(AD2+AB2).其中正確的是 ,并給出證明.
AD;②BE2=2(AD2+AB2).其中正確的是 ,并給出證明.
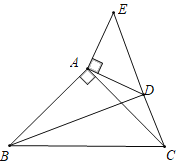
(2)若AB=4,AD=2,把△ADE繞點A旋轉,
①當∠EAC=90°時,求PB的長;
②旋轉過程中線段PB長的最大值是 .
【答案】(1)①,證明詳見解析;(2)①PB=![]() ;②2
;②2![]() +2.
+2.
【解析】
(1)①由條件證明△ABD≌△ACE,就可以得到結論;②△BDE為直角三角形就可以得出BE2=BD2+DE2,由△DAE和△BAC是等腰直角三角形就有DE2=2AD2,BC2=2AB2,就有BC2=BD2+CD2≠BD2就可以得出結論;
(2)分兩種情形當點E在AB上時,BE=AB﹣AE=2.由△PEB∽△AEC,得![]() ,由此即可解決問題;當點E在BA延長線上時,BE=6.解法類似;
,由此即可解決問題;當點E在BA延長線上時,BE=6.解法類似;
②如圖3中,以A為圓心AD為半徑畫圓,當CE在⊙A上方與⊙A相切時,PB的值最大.分別求出PB即可;
(1)∵△ABC和△ADE是有公共頂點的等腰直角三角形,
∴AE=AD,AB=AC,∠DAE=∠BAC=90°,DE=![]() AD,
AD,
∴∠DAB=∠EAC,且AE=AD,AB=AC,
∴△AEC≌△ADB(SAS)
∴BD=CE=DE+CD,
∴BD=CD+![]() AD,
AD,
∴①正確,
∵BD⊥CE,
∴BE2=BD2+DE2,
∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴DE2=2AD2,BC2=2AB2,
∵BC2=BD2+CD2≠BD2,
∴2AB2=BD2+CD2≠BD2,
∴BE2≠2(AD2+AB2),
∴②錯誤.
故答案為①;
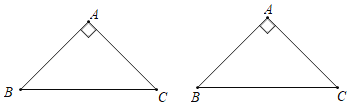
(2)①圖1中,當點E在AB上時,BE=AB﹣AE=2.
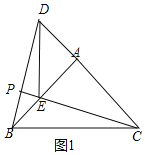
∵∠EAC=90°,
∴CE=![]() =
=![]() =2
=2![]() ,
,
同(1)可證△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠PEB=∠AEC,
∴△PEB∽△AEC.
∴![]() ,
,
∴![]()
∴PB=![]() .
.
如圖2中,當點E在BA延長線上時,BE=AB+AE=6.

∵∠EAC=90°,
∴CE=![]() =
=![]() =2
=2![]() ,
,
同(1)可證△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB=![]() ,
,
綜上,PB=![]() 或
或![]() ;
;
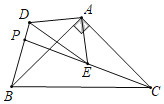
②如圖3中,以A為圓心AD為半徑畫圓,當CE在⊙A上方與⊙A相切時,PB的值最大.
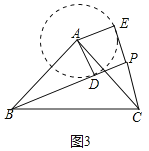
理由:此時∠BCE最大,因此PB最大,(△PBC是直角三角形,斜邊BC為定值,∠BCE最大,因此PB最大)
∵AE⊥EC,
∴EC=![]() =
=![]() =2
=2![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE=2![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四邊形AEPD是矩形,
∴PD=AE=2,
∴PB=BD+PD=2![]() +2,
+2,
綜上所述,PB長的最大值是2![]() +2,
+2,
故答案為:2![]() +2.
+2.


科目:初中數學 來源: 題型:
【題目】![]() 兩地相距
兩地相距![]() ,甲、乙兩人從兩地出發相向而行,甲先出發.圖中
,甲、乙兩人從兩地出發相向而行,甲先出發.圖中![]() 表示兩人離
表示兩人離![]() 地的距離
地的距離![]() 與時間
與時間![]() 的關系,結合圖象,下列結論錯誤的是( )
的關系,結合圖象,下列結論錯誤的是( )
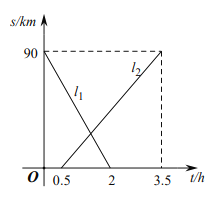
A.![]() 是表示甲離
是表示甲離![]() 地的距離與時間關系的圖象
地的距離與時間關系的圖象
B.乙的速度是![]()
C.兩人相遇時間在![]()
D.當甲到達終點時乙距離終點還有![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 是
是![]() 邊上的動點(不與
邊上的動點(不與![]() 重合),點
重合),點![]() 在
在![]() 邊上,并且滿足
邊上,并且滿足![]() .
.
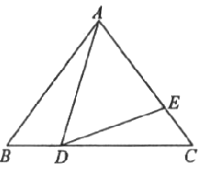
(1)求證:![]() ;
;
(2)若![]() 的長為
的長為![]() ,請用含
,請用含![]() 的代數式表示
的代數式表示![]() 的長;
的長;
(3)當(2)中的![]() 最短時,求
最短時,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,線段![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為射線
為射線![]() 上一點,
上一點,![]() 平分
平分![]() 交線段
交線段![]() 于點
于點![]() (不與端點
(不與端點![]() ,
,![]() 重合).
重合).

(1)當![]() 為銳角,且
為銳角,且![]() 時,求四邊形
時,求四邊形![]() 的面積;
的面積;
(2)當![]() 與
與![]() 相似時,求線段
相似時,求線段![]() 的長;
的長;
(3)設![]() ,
,![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并寫出定義域.
的函數關系式,并寫出定義域.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() ,
,![]() (如圖),點
(如圖),點![]() ,
,![]() 分別為射線
分別為射線![]() 上的動點(點C、E都不與點B重合),連接AC、AE使得
上的動點(點C、E都不與點B重合),連接AC、AE使得![]() ,射線
,射線![]() 交射線
交射線![]() 于點
于點![]() ,設
,設![]() ,
,![]() .
.
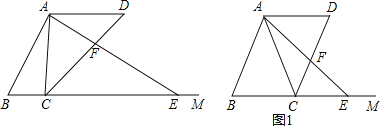
(1)如圖1,當![]() 時,求AF的長.
時,求AF的長.
(2)當點![]() 在點
在點![]() 的右側時,求
的右側時,求![]() 關于
關于![]() 的函數關系式,并寫出函數的定義域.
的函數關系式,并寫出函數的定義域.
(3)連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() 是等腰三角形,直接寫出
是等腰三角形,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
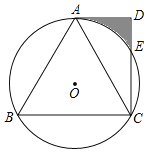
【題目】如圖,⊙O為等邊△ABC的外接圓,AD∥BC,∠ADC=90°,CD交⊙O于點E.
(1)求證:AD是⊙O的切線;
(2)若DE=2,求陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某縣建檔立卡貧困戶對精準扶貧政策落實的滿意度,現從全縣建檔立卡貧困戶中隨機抽取了部分貧困戶進行了調查(把調查結果分為四個等級:A級:非常滿意:B級滿意;C級:基本滿意:D級:不滿意),并將調查結果繪制成如兩幅不完整的統計圖,請根據統計圖中的信息解決下列問題:
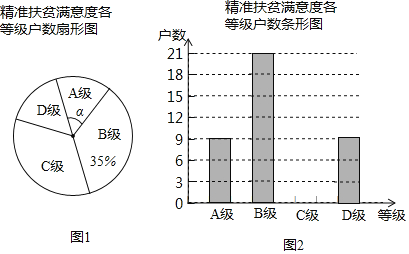
(1)本次抽樣調查測試的建檔立卡貧困戶的總戶數是 ;
(2)圖①中,∠α的度數是 ,并把圖②條形統計圖補充完整;
(3)某縣建檔立卡貧困戶有10000戶,如果全部參加這次滿意度調查,請估計非常滿意的戶數約為多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,以
中,以![]() 為圓心作⊙
為圓心作⊙![]() ,⊙
,⊙![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,![]() 為⊙
為⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一點,連接
的任意一點,連接![]() 、
、![]() ,過
,過![]() 點分別作
點分別作![]() 于
于![]() ,
,![]() 于
于![]() .設點
.設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() .當
.當![]() 點在⊙
點在⊙![]() 上順時針從點
上順時針從點![]() 運動到點
運動到點![]() 的過程中,下列圖象中能表示
的過程中,下列圖象中能表示![]() 與
與![]() 的函數關系的部分圖象是( )
的函數關系的部分圖象是( )

A.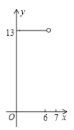 B.
B.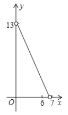 C.
C.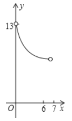 D.
D.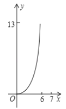
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com